Conoce la ecuación de una parábola La ecuación de una parábola es y = ax 2 bx cTambién se puede escribir de la siguiente manera y = a(x – h)2 k, pero este ejemplo se enfocará en la primera forma de la ecuación Si la a en la ecuación es positiva, entonces la parábola se abre hacia arriba, como una "U" y tiene un punto mínimo Si la a es negativa, entonces se abre haciaFUNCIÓN CUADRÁTICA 2 Sergio Signorelli PROHIBIDA SU REPRODUCCION Mientras que si el valor de a es negativo las ramas apuntarán hacia abajo El valor de c, también es muy importante dentro de la función, pues indica adonde ha de cortar la parábola el eje de las y (similar al valor de la b en la función lineal) A este valor, al de c, también se lo llama ordenada al origenEn matemáticas, una parábola es una curva plana que es simétrica y está aproximadamente U formaSe ajusta a varias descripciones matemáticas superficialmente diferentes , que se puede probar que definen exactamente las mismas curvas Una descripción de una parábola involucra un punto (el foco) y una línea (la directriz)El foco no está en la directriz
Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola
Parabola equation y=ax^2
Parabola equation y=ax^2-In mathematics, a parabola is a plane curve which is mirrorsymmetrical and is approximately UshapedIt fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves One description of a parabola involves a point (the focus) and a line (the directrix)The focus does not lie on the directrixEs decir, aunque cambiemos los valores de b b y de B B, las rectas y = a x b y = a x b e y = − 1 a x B y = − 1 a x B son perpendiculares 4 Problemas sobre parábolas Problema 1 Calcular los puntos de corte de la siguiente parábola con los ejes de coordenadas Solución



Vertex Form How To Find The Equation Of A Parabola
Click here👆to get an answer to your question ️ The vertex of the parabola y = ax^2 bx c isLa gráfica de las funciones polinómicas de segundo grado o funciones cuadráticas son las parábolas4 La gráfica de una función cuadrática f(x) = ax2 bx c es una parábola 5 La parábola abre hacia arriba si a > 0 y abre hacia abajo si a < 0 Conceptos clave Si trabajamos un poco en la función cuadrática y = ax2 bx c, como lo hicimos cuando llevamos la ecuación general de una parábola vertical a la forma ordinaria ax2 bx c =
La parábola La función cuadrática o parábola es de la forma y =ax2 bx c tal que a ≠0 La orientación de la parábola depende del signo de a ⎩ ⎨ ⎧ < → > → a 0 ramas hacia abajo función convexa a 0 ramas hacia arriba función cóncava El eje de simetría viene dado por la recta 2a b x − = El vértice de la parábola tieneLa parábola de ecuación y=ax 2 bxc (Ecuación completa de la parábola ) Vamos a ver, por fin, la ecuación completa de la parábola, es decir la parábola cuya ecuación es y= a x 2 b x c , donde a , b y c son números reales distintos de ceroConstrucción del incentro de un triángulo
Equivalencia entre grados y radianesParabola y=ax^2 Create ClassAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators
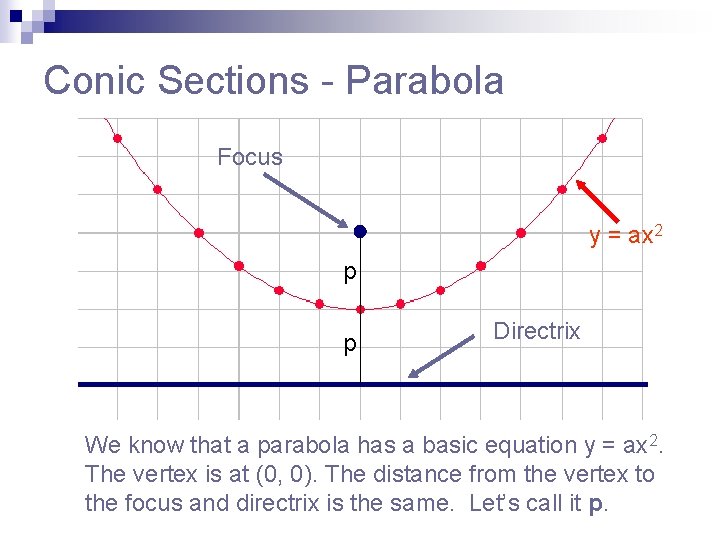



Conic Sections 11 1 Parabola Conic Sections Parabola
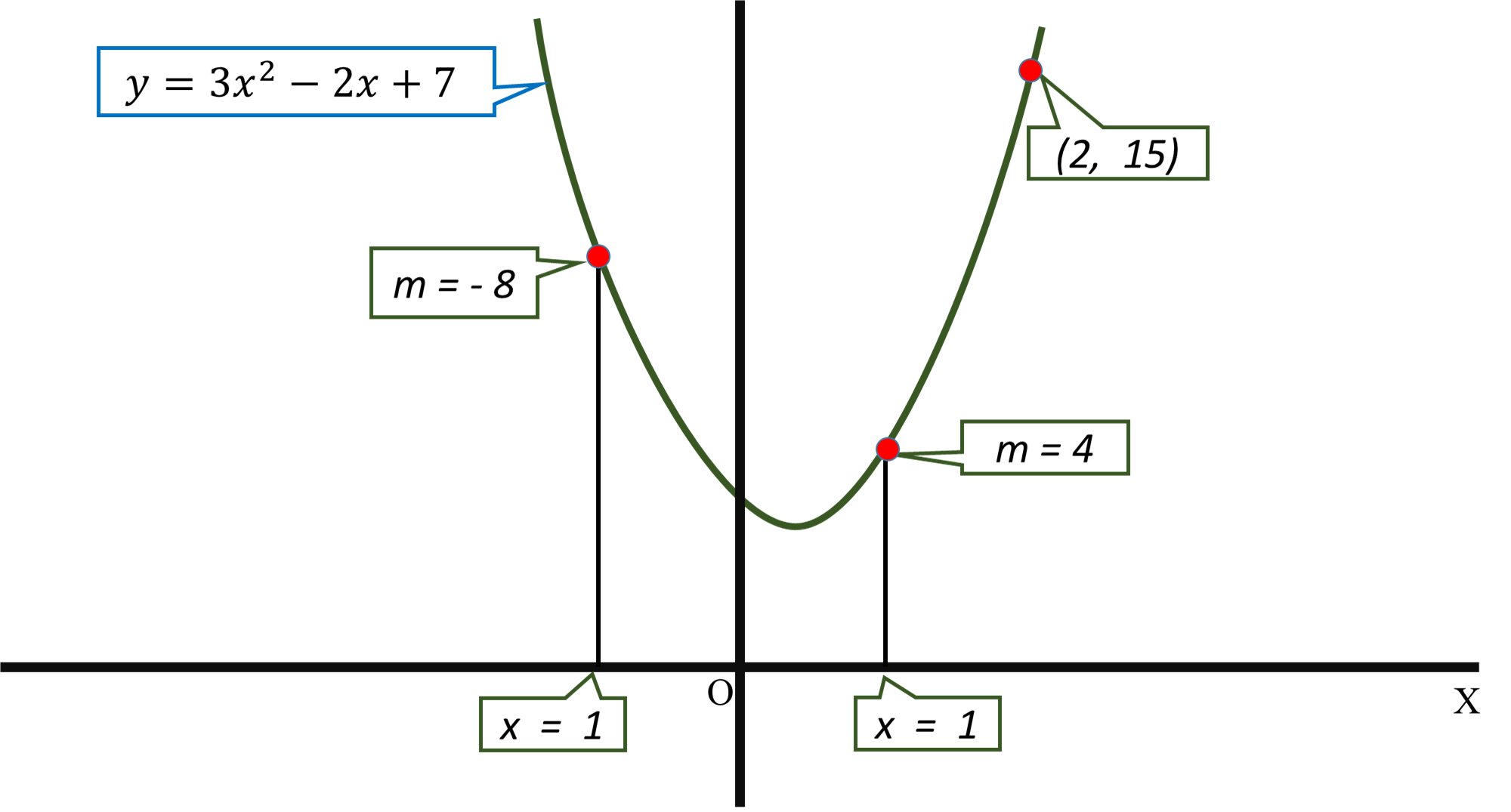



How Do You Find A Parabola With Equation Y Ax 2 Bx C That Has Slope 4 At X 1 Slope 8 At X 1 And Passes Through 2 15 Socratic
2/6/21 Parábola Parábola y=ax^2bxc Comprueba como varía su gráfica al variar los valores de a, b y c con los deslizadoresEn esta escena puedes ver representada la parábola y = ax 2 bx c, donde puedes cambiar los valores de a, b y c EJERCICIO 4 Anota en tu cuaderno a) Partiendo del inicio de la escena, deja fijos b y c, y cambia los valores de a (sin limpiar), dando valores positivos, así obtendrás una familia de parábolas ¿Cómo influyenEjemplo paso a paso Vamos a graficar una línea de la forma y=mxb Comenzamos con una hoja nueva de Excel Escribe en la celda B2 la oración "Pendiente m=" y en la celda la oración "Ordenada b=" Las celdas C2 y C3 van a ser usadas para los valores numéricos de m y b Para indicar que estas celdas son especiales, vamos a colorearla de amarillo
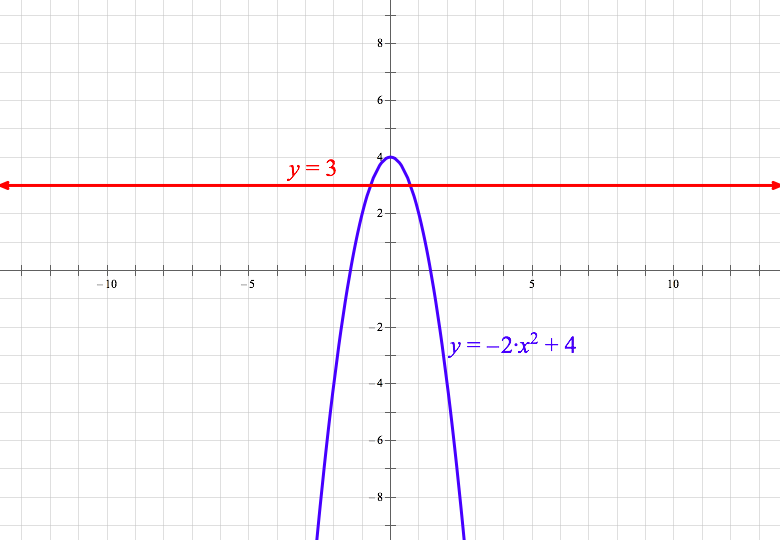



Pwn Test Prep Sat Q A Satpracticetest2 Qn 29 Y 3 Y Ax 2 B In




The Graphs Of Y Ax 2 Bx C Are Given In Figure Identify The Signs Of A B And C In Each Of The Following
Un resultado importante La forma de una parábola depende única y exclusivamente del coeficiente a de x 2, es decir, cualquier parábola del tipo y = ax 2 bx c tiene la misma forma que la parábola y = ax 2 Por ejemplo La parábola y = 2x 216x 35 tiene la misma forma que y = 2x 2;La expresión algebraica que describe una parábola que ocupe cualquier posición en un plano es a x 2 b x y c y 2 d x e y f = 0 {\displaystyle \,ax^ {2}bxycy^ {2}dxeyf=0} si y solo si b 2 − 4 a c = 0 {\displaystyle \,b^ {2}4ac=0} y los coeficientes aEncajan perfectamente una encima de la otra como puedes comprobar si dibujas las dos parábolas



Suppose A Parabola Y Ax 2 Bx C Has Two X Intercepts One Positive And One Negative And Its Vertex Is 2 2 Sarthaks Econnect Largest Online Education Community




Chapter 9 Quadratic Functions And Equations Flashcards Quizlet
19/5/18 #color(blue)(y=ax^2bxc# Graph of a quadratic function forms a Parabola The coefficient of the #color(red)(x^2# term (a) makes the parabola wider or narrow If the coefficient of the #color(red)(x^2,# term (a) is negative then the parabola opens down The term Vertex is used to identify the Turning Point of a parabolaParábola y=ax^2 – GeoGebraRecuerda que una parábola es de la forma $y=ax^2bxc$ Actividad de ejemplo En este programa hay una función llamada f()a la que le pasamos los valores a, b, c, xy calcula el valor de la función Antes de hacer nada vamos a ver un ejemplo concreto para asegurarnos de que todo está bien claro Por ejemplo, tenemos la parábola $y=2x^23x1$ y
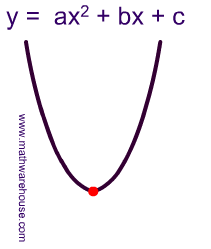



Standard And Vertex Form Of The Equation Of Parabola And How It Relates To A Parabola S Graph




Graphing A Parabola Of The Form Y Ax 2 Bx C With Integer Coefficients Practice Study Com
Parábola y = ax2se desplaza k unidades hacia arriba• Los elementos más importantes de una parábola son el vértice y el eje de simetría Vamos, a continuación, a obtener las coordenadas V = (x v , y v) del vértice y la ecuación del eje de simetría de la parábola de ecuación y = ax 2 bx c Las coordenadas de los puntos en los que la parábola y = ax2 bx cLa parábola de ecuación y=ax 2 Decimos que la ecuación de esta parábola es incompleta, esto se debe a que no aparecen los términos b x y c , es decir b = c= 0 Deberás ser tú, quién vaya escribiendo en su cuaderno las propiedades, a partir de las cuestiones y la experimentación que te proponemos a continuación




Mfg Graphing Parabolas
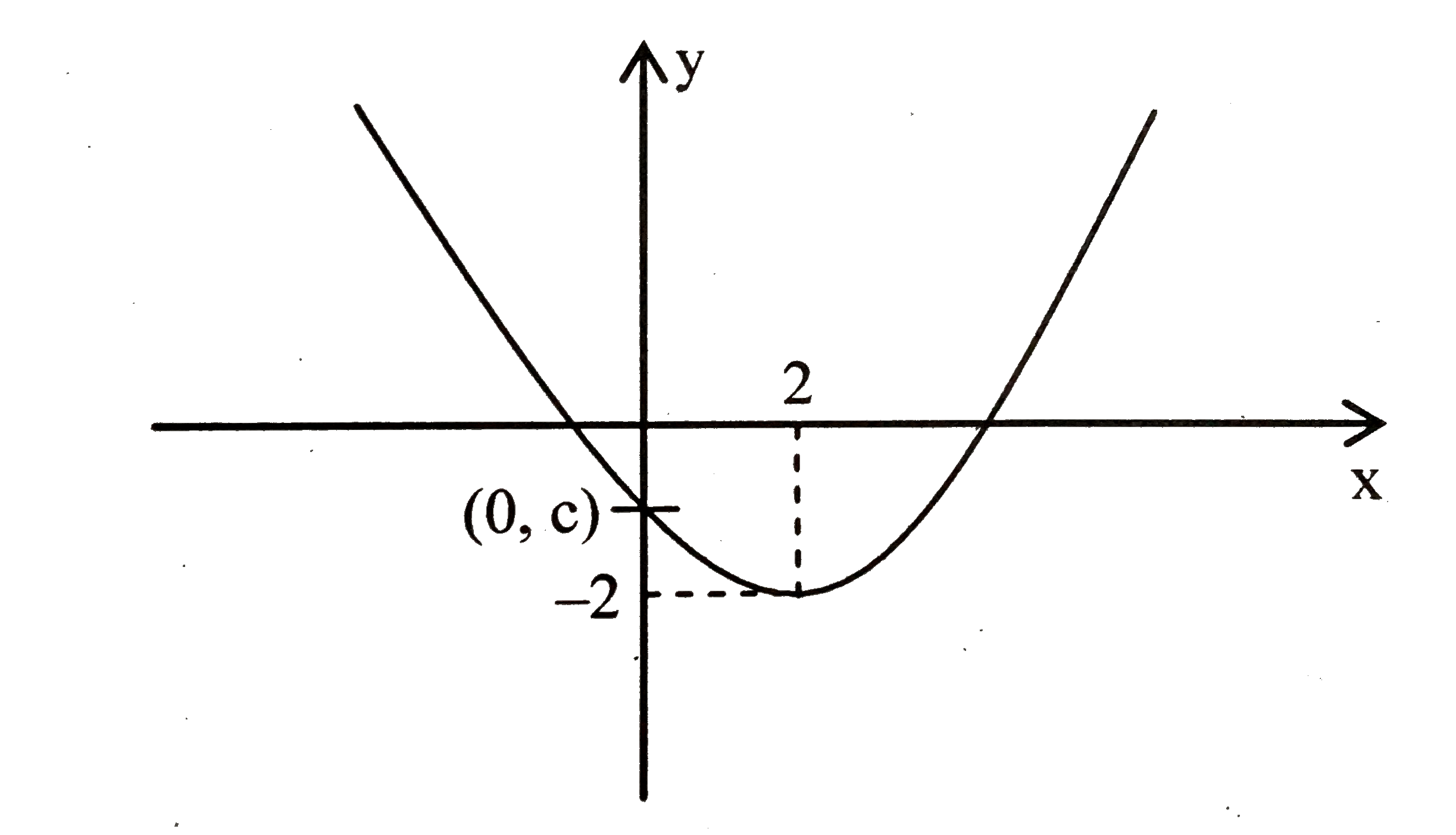



Suppose A Parabola Y Ax 2 Bx C Has Two X Intercepts One Pos
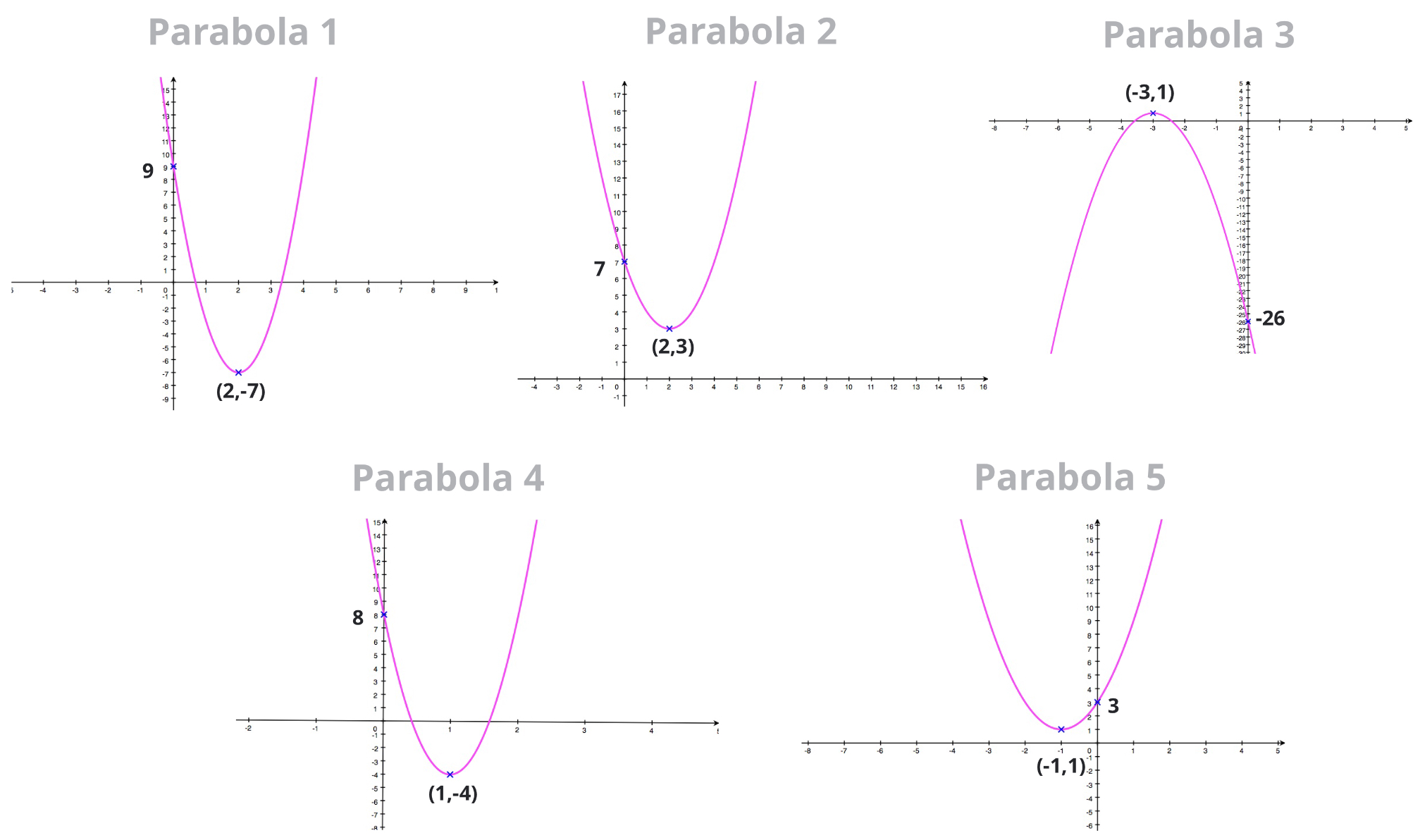
Y = a x 2 b x c In this exercise, we will be exploring parabolic graphs of the form y = a x 2 b x c, where a, b, and c are rational numbers In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the thirdStart asking, answering, commenting and voting on MathsGee Answers platform MathsGee Answers is a global, STEMfocused Q&A platform where you can ask people from all over the world educational questions for improved outcomes The given parabola y = ax2 bx c y = a x 2 b x c doesn't intersect the Xaxis and passes from the points A(−2 Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange
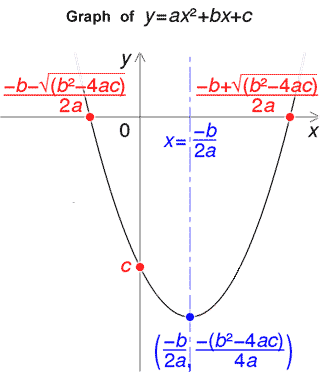



Quadratic Formula Calculator
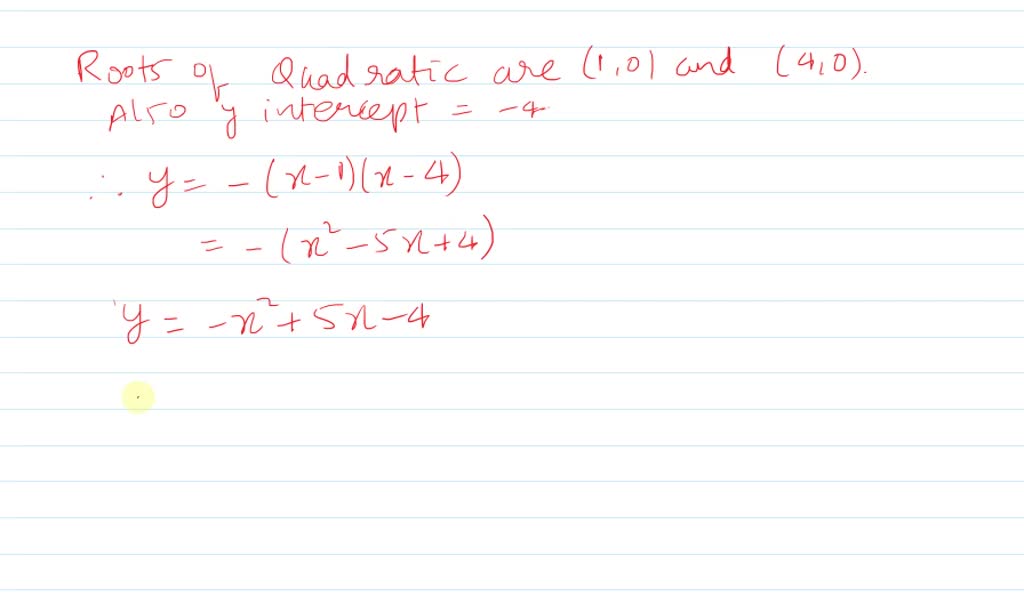



Solved Writing The Parabola In The Figure Below H
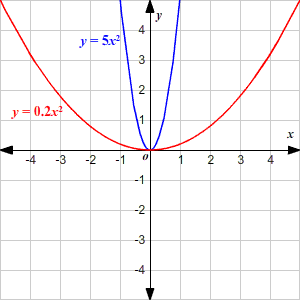
PARABOLA y=ax^2bxc con delta nullo 1157 PARABOLA 10 videos matematicale SUBSCRIBE SUBSCRIBED You're signed out Videos you watch may be added to the TV's watch history and influence TVUna parábola cuyo vértice está en el origen y su eje coincide con el eje de las ordenadas, tiene una ecuación de la forma y = ax 2 donde el parámetro a especifica la escala de la parábola, incorrectamente descrita como la forma de la parábola, ya que como se dijo antes, todas las parábolas tienen la misma formaFamilia de parábolas Las gráficas de las funciones de ecuación y = ax2 bx c son parábolas de eje vertical En la escena siguiente del nippe Descartes puedes ver representada la parábola y = ax 2 bx c, donde puedes cambiar los valores de a, b y c Prueba con diferentes valores para a, b y c y trata de interpretar los resultados
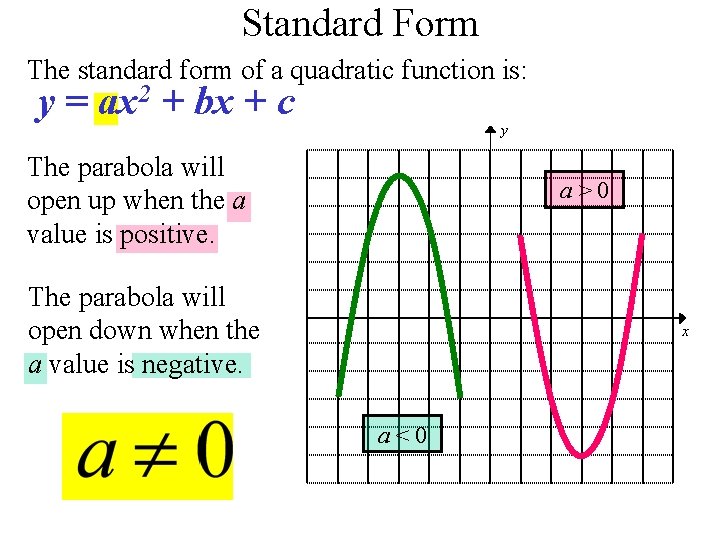



Quadratic Function Y Ax 2 Bx C Quadratic




J 4 Y 1 0 13 Focus Of Parabola Y Ax2 Bx C Is
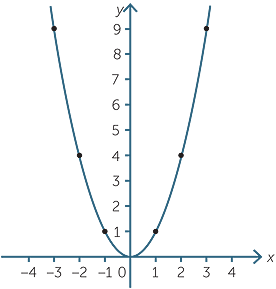
Scribd is the world's largest social reading and publishing site Lado recto y En otras palabras, la parábola es una curva abierta y plana que se presenta como el lugar geométrico de los puntos del plano que se encuentran equidistantes de un punto denominado foco (punto fijo), y una recta denominada directriz (línea fija) Distancia focal 3) El vértice de una parábola se ubica en Estudio gráfico de la función y = ax^2 Este tipo de funciones en las que x aparece con exponente 2 se caracterizan por tener como representación gráfica una línea curva, simétrica, de forma parabólica, cualquiera que sea el valor que tome a Por otro lado, al carecer de término independiente, necesariamente pasará por el origen deEn esta escena puedes ver representada la parábola y = ax 2 bx c, donde puedes cambiar los valores de a, b y c EJERCICIO 4 Anota en tu cuaderno a) Partiendo del inicio de la escena, deja fijos b y c, y cambia los valores de a (sin limpiar), dando valores positivos, así obtendrás una familia de parábolas ¿Cómo influyen estos
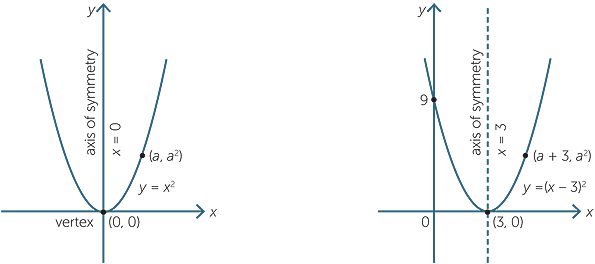



Quadratic Function
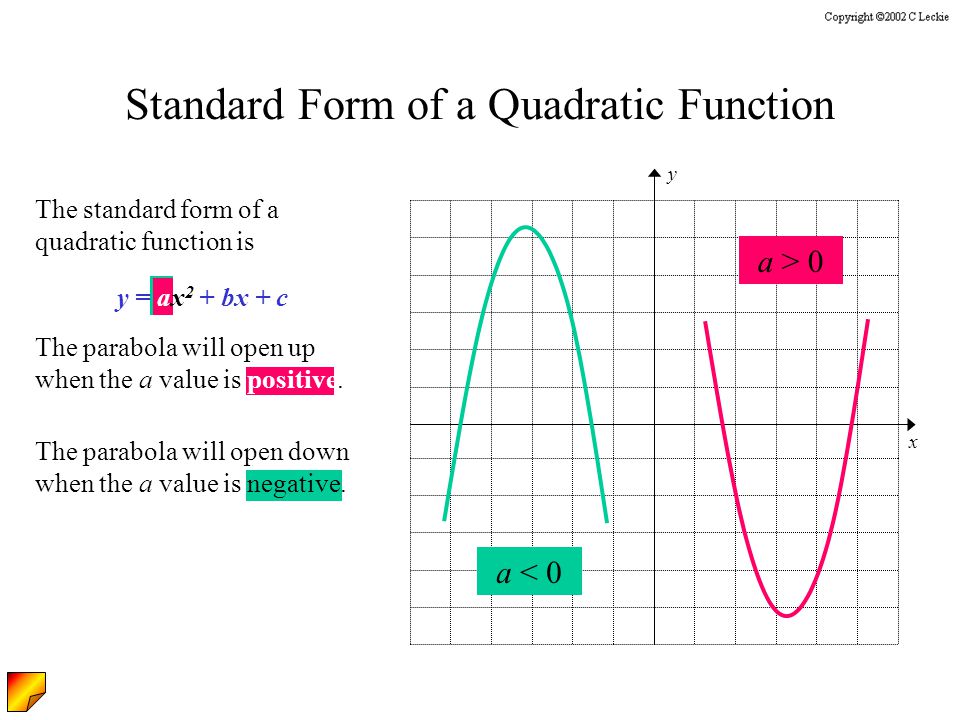



Lesson 10 2 Quadratic Functions And Their Graphs Y Ax 2 Bx C Ppt Download
Un esempio di parabola con il vertice sull'asse delle y che non ha intersezioni con l'asse delle y📱FACEBOOK https//wwwfacebookcom/matematicale📱INSTAGRAGraphing Parabolas in the Form y = ax^2 Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device Up next in 8La parabola Parte I Equazione della parabola y=ax^2 Watch later Share Copy link Info Shopping Tap to unmute wwwgrammarlycom If playback doesn't begin shortly, try
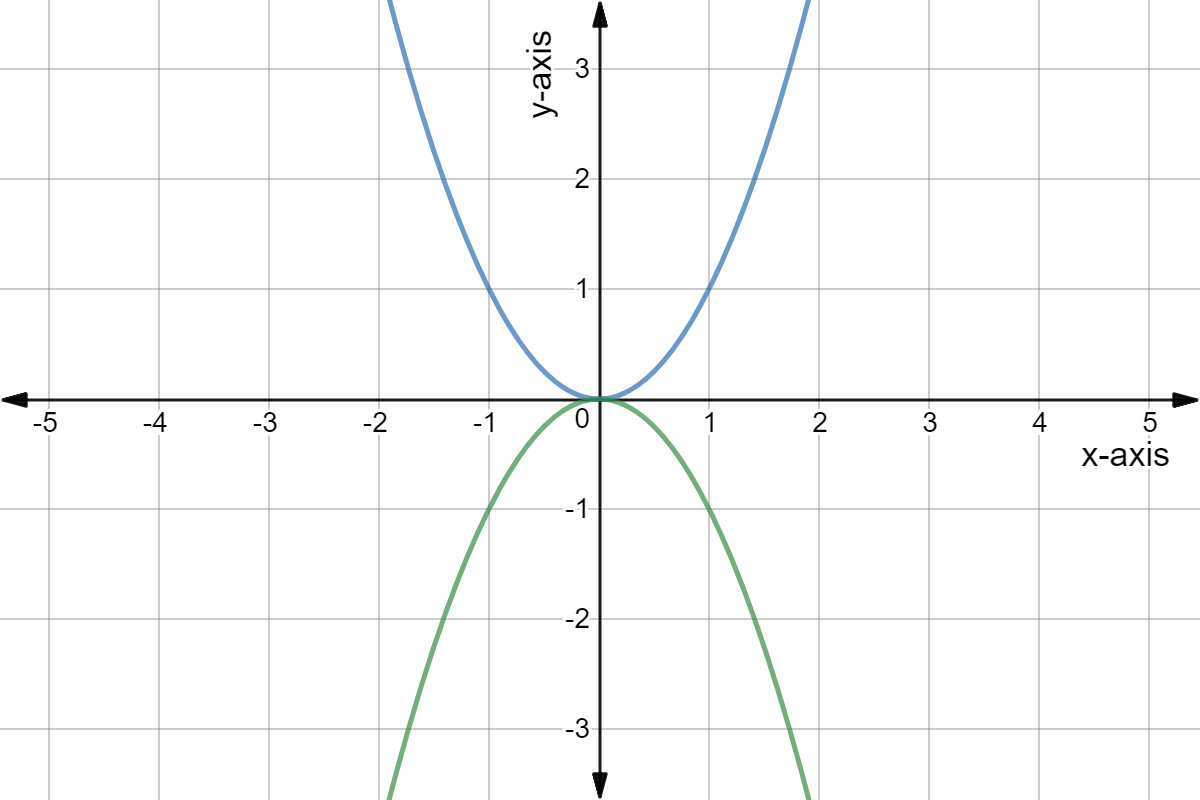



Quadratic Graph Example Y Ax Expii
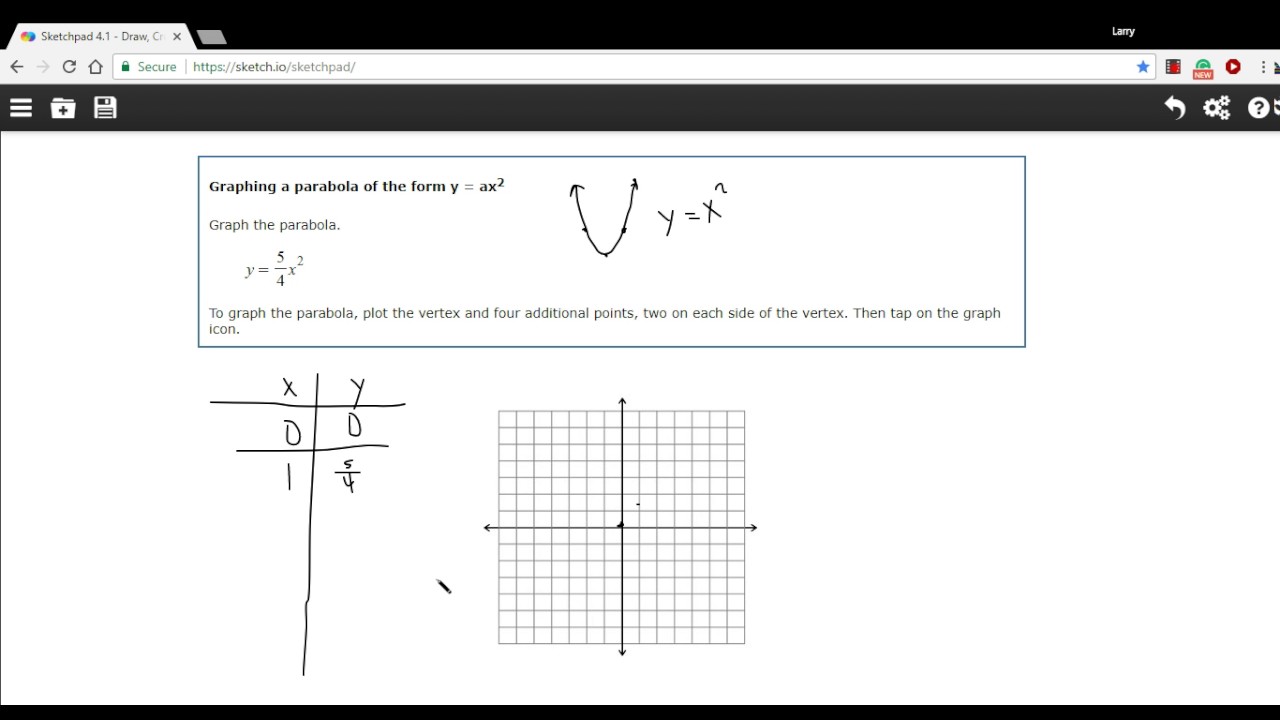



Graphing A Parabola In The Form Of Y Ax Squared Youtube
Función La parábola es la gráfica de toda función asociada a un polinomio de segundo grado, es decir y=f(x)=ax2bxc Veamos casos particulares 321 Función parabólica del tipo y=ax2 Si tenemos la función y=f(x)=ax2 Para entender como es la parábola en función del parámetro a veamos 4 casos distintosLa curvatura máxima de una parábola se da en su vértice, para la parábola que das el vértice está en x = − b / 2 a Hay varias maneras de calcular la curvatura, especializando para curvas planas tipo y = f (x) χ = f ″ (x) 1 (f ′ (x)) 2 3 / 2 Si aplicamos esa fórmula a la parábola que das χ = 2 a 1 (2 a x b) 2 3 / 2 ≤ 2 a = χ maxEn esta ecuación, el vértice de la parábola es el punto ( h , k ) Puede ver como se relaciona esto con la ecuación estándar al multiplicar y = a ( x – h ) ( x – h ) k y = ax 2 – 2 ahx ah 2 k El coeficiente de x aquí es – 2 ah Esto significa que en la forma estándar, y = ax 2 bx c , la expresión da la coordenada
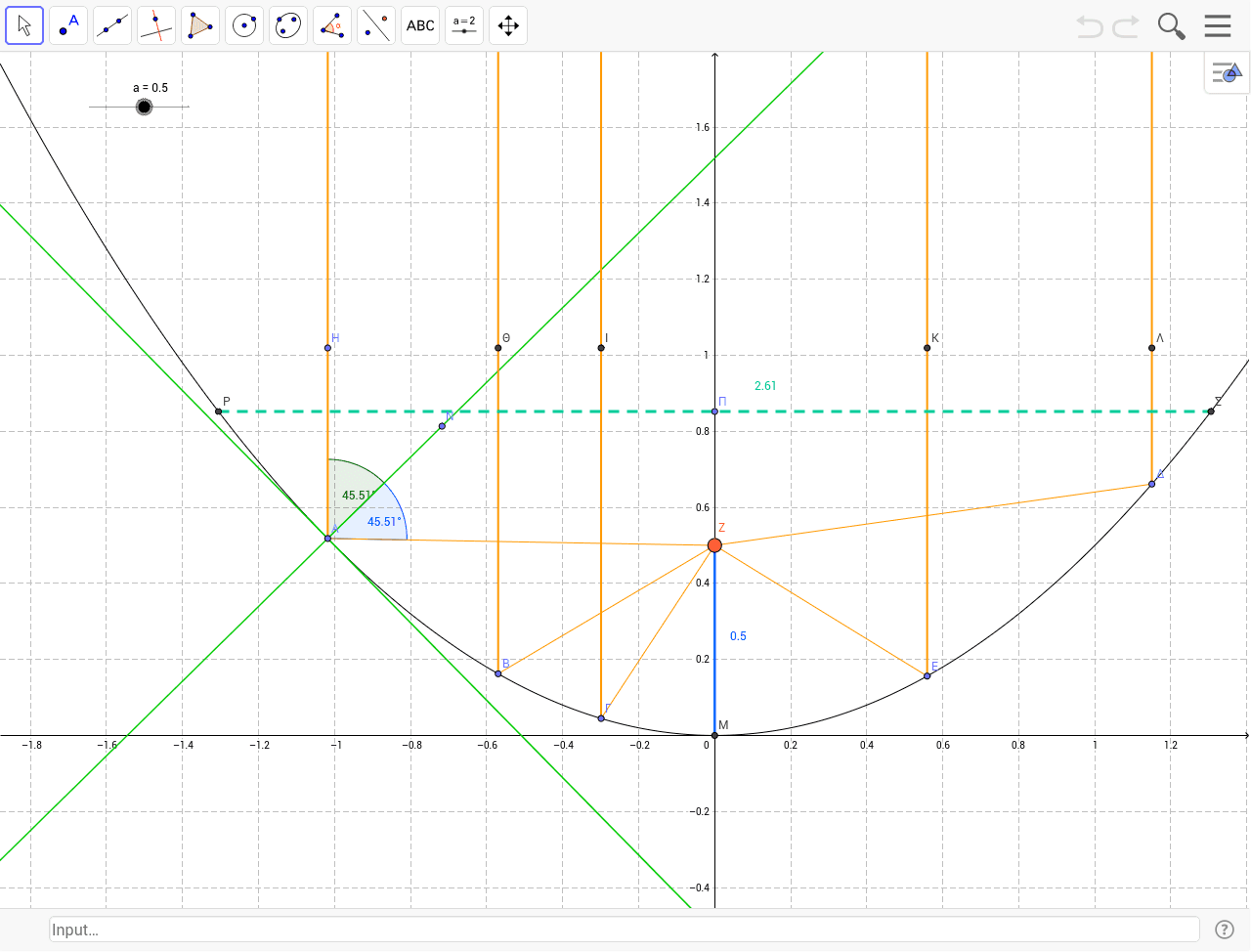



Parabola Y Ax 2 Geogebra




Which Of The Following Is An Equation In The Form Y Ax2 Bx C Of The Parabola Shown In The Brainly Com
Examining the Parabola (Assignment 2) by Robin Kirkham, Cara Haskins , and Matt Tumlin _____ Let us examine the parabola as the coefficient values change to see the effects these changes have on the various parabolas Given the parabola y = ax 2 bx c with variables of a, b, and cLa parábola de ecuación y=ax^2bx La parábola de ecuación y=ax2bx (desplazamiento del eje de simetría de la parábola) De nuevo, la ecuación de esta parábola también es incompleta Ahora falta el término c;Arguably, y = x^2 is the simplest of quadratic functions In this exploration, we will examine how making changes to the equation affects the graph of the function We will begin by adding a coefficient to x^2 The movie clip below animates the graph of y = nx^2 as n changes between 10 and 10 As you can see in the animation, the value of n
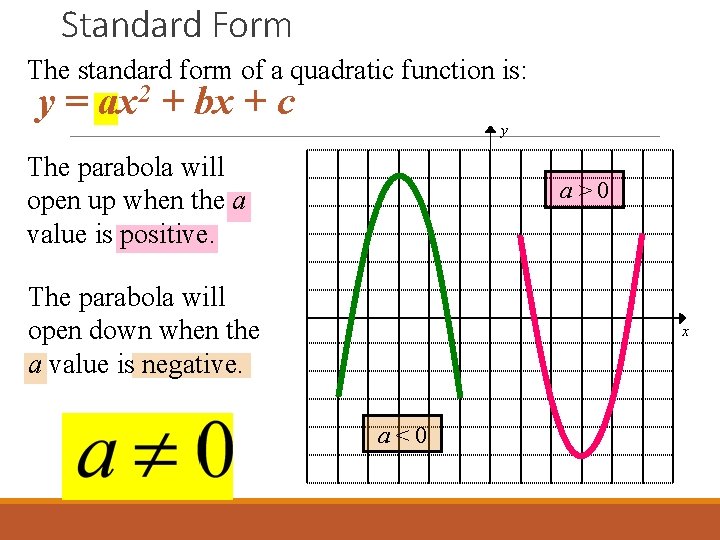



Graphing Quadratic Functions Ma 912 A 7 1
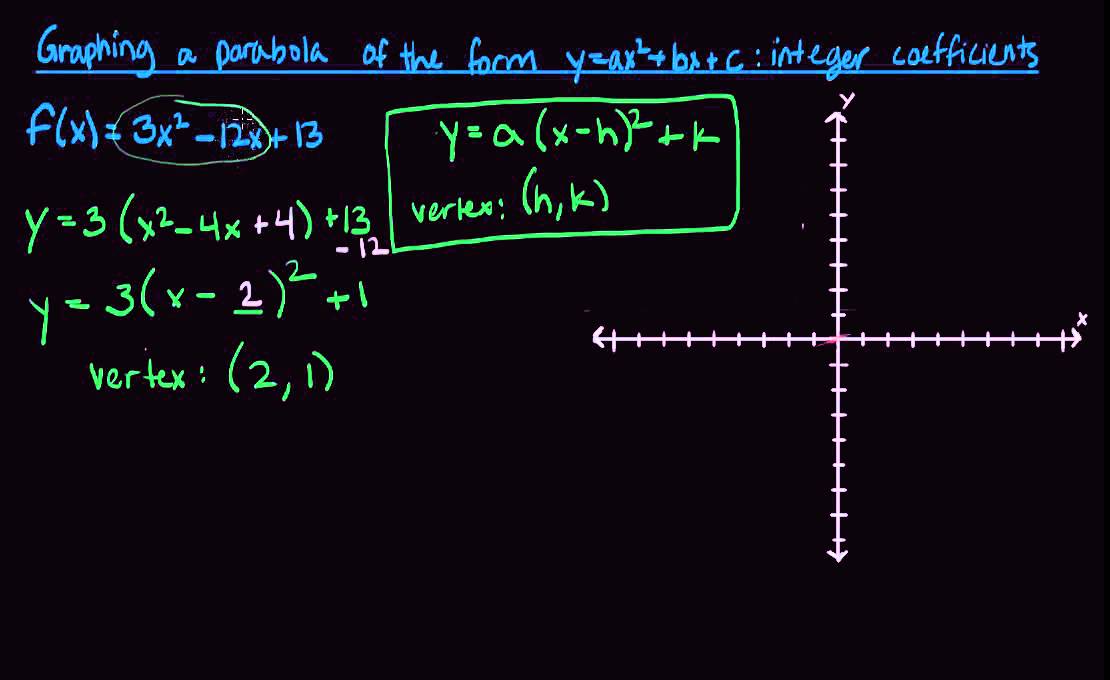



Graphing A Parabola Of The Form Y Ax2 Bx C With Integer Coefficients Youtube
Si es una parábola que se abre hacia arriba el valor de c es c = − 2 El valor de a tiene que ser menor que el radio de curvatura de la parábola De acuerdo con la ecuación de la parábola, su radio de curvatura cuando x = 0 para esta parábola en particular es ρ = 1 2 a Como en este caso particular ρ = 2 Solamente queda igualar29/6/ Determinar la ecuación de la parabola y=ax^2bxc que pasa por (0,1) y es tangente a la recta y=x1 en (1,0) 1 Ver respuesta YeseniaJ está esperando tu ayuda Añade tu respuesta y gana puntos Justo63br Justo63br Determinación de la ecuación de la parábola con las condiciones dadasY=ax^2bxc Parabola Descubrir recursos Catenaria Sagrada Família;
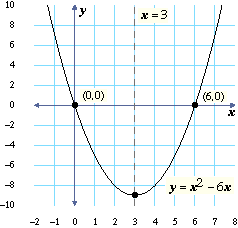



Investigating Y Ax 2 Bx
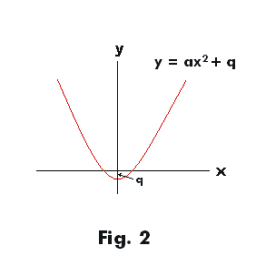



The Function F X Y And Associated Matrices E And E
Parábola y=ax^2bxc Descubrir recursos Jorge Martinez; Estudio gráfico de la función de tipo y = ax^2 bx c Tanto este tipo de función como las dos anteriores ( aquí y aquí ), son funciones de segundo grado Por tanto, su representación gráfica será también una parábola, que como en el caso anterior nunca pasará por el origen de coordenadasY ax2 =4 Esta es la ecuación de una parábola con el vértice en el origen y foco en ( −a, 0) En esta última expresión como a < 0, la variable x sólo puede tomar valores negativos para que la expresión última y 2 = 4ax, tenga sentido En resumen podemos afirmar "La ecuación de una parábola con vértice en el origen y foco
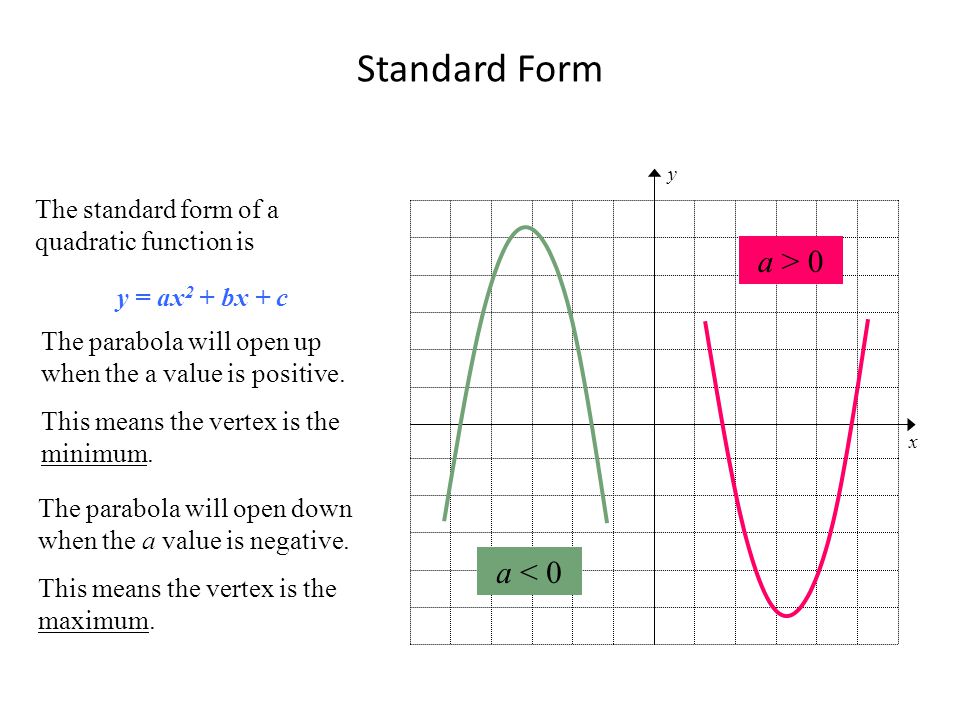



Topic U2 L1 Parts Of A Quadratic Function Graphing Quadratics Y Ax 2 Bx C Eq Can I Identify The Vertex Axis Of Symmetry X And Y Intercepts Ppt Download



Quadratics
La envolvente de todas las trayectorias descritas por los proyectiles cuyo ángulo de disparo está comprendido entre 0 y 180º se denomina parábola de seguridad Se trata de la parábola simétrica respecto del eje Y de ecuación y=ax 2 b que pasa por los puntos (x=v 0 2 /g, y=0), y (x=0, y=v 0 2 /(2g)) tal como se ve en la figuraIn the next few questions, we will find the roots of the general equation y = a x 2 b x with a ≠ 0 by factoring, and use that to get a formula for the axis of symmetry of any equation in that form Question 5 We want to factor a x 2 b x Because both terms contain an



Parabola




Quadratic Function Wikipedia
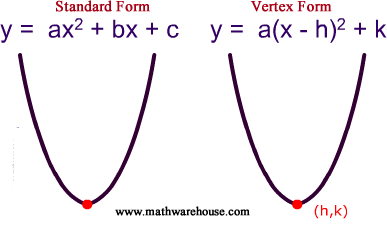



Standard And Vertex Form Of The Equation Of Parabola And How It Relates To A Parabola S Graph



Q Tbn And9gcskitjvtu4g6u7oh5r8z42jlb391urt3idlmfdbjguuxli7v2fo Usqp Cau
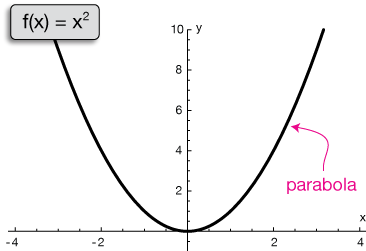



Quadratic Function Y Ax2 Bx C When A Is Sutori
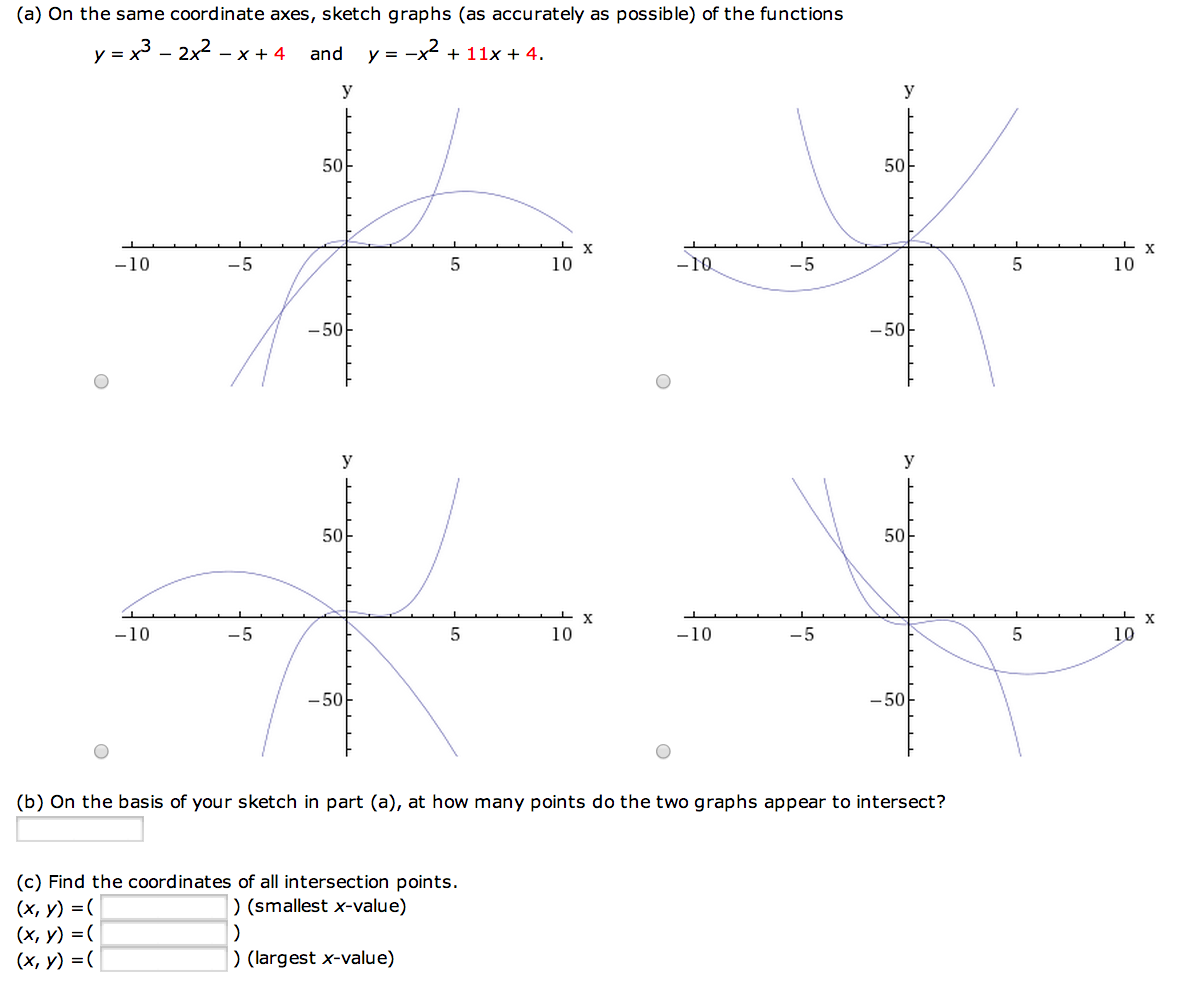



Find A Parabola With Equation Y Ax2 Bx C That Chegg Com



1



Quadratics



How To Determine A Quadratic Function Y Ax 2 Bx C If Its Graph Passes Through The Point 2 19 And It Has A Horizontal Tangent At 1 8 Quora




Number Of A Parabola Of The Form Y Ax 2 Bx C With A 0 Int




Graphing Quadratic Functions Lesson Article Khan Academy




Graphing A Parabola Of The Form Y Ax2 C Practice Study Com
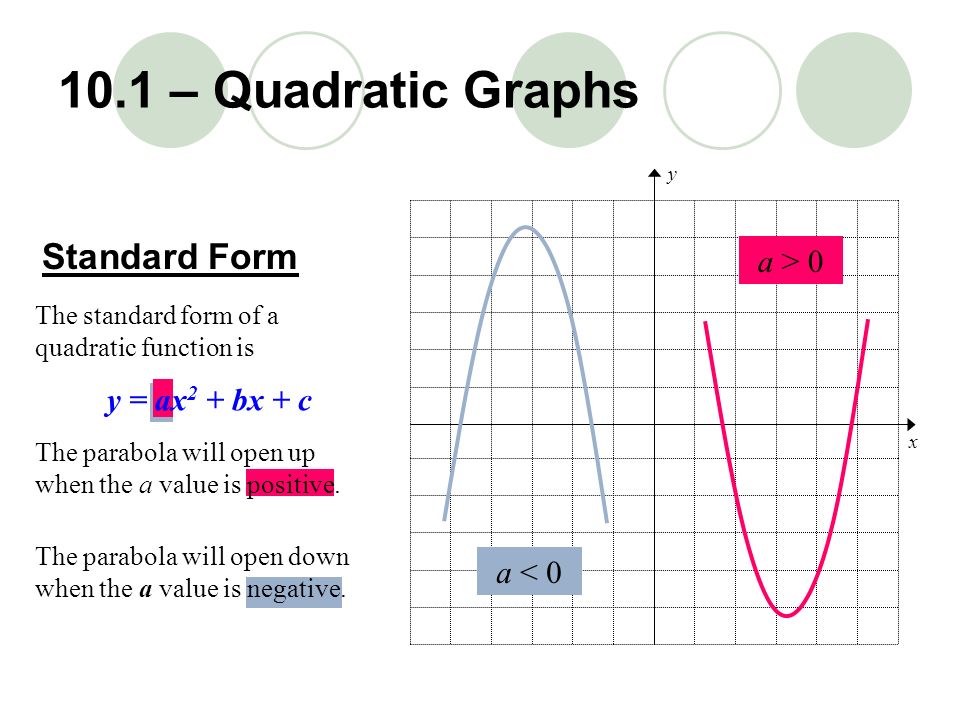



10 1 Quadratic Graphs Ppt Download
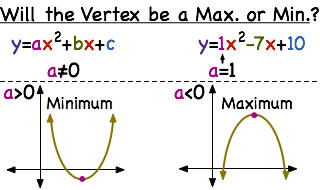



How Do You Determine If The Vertex Will Be A Maximum Or Minimum Printable Summary Virtual Nerd



Sat Math Multiple Choice Question 2 Answer And Explanation Cracksat Net



Quadratic Function



Parabolas




Quadratic Functions Functions Siyavula
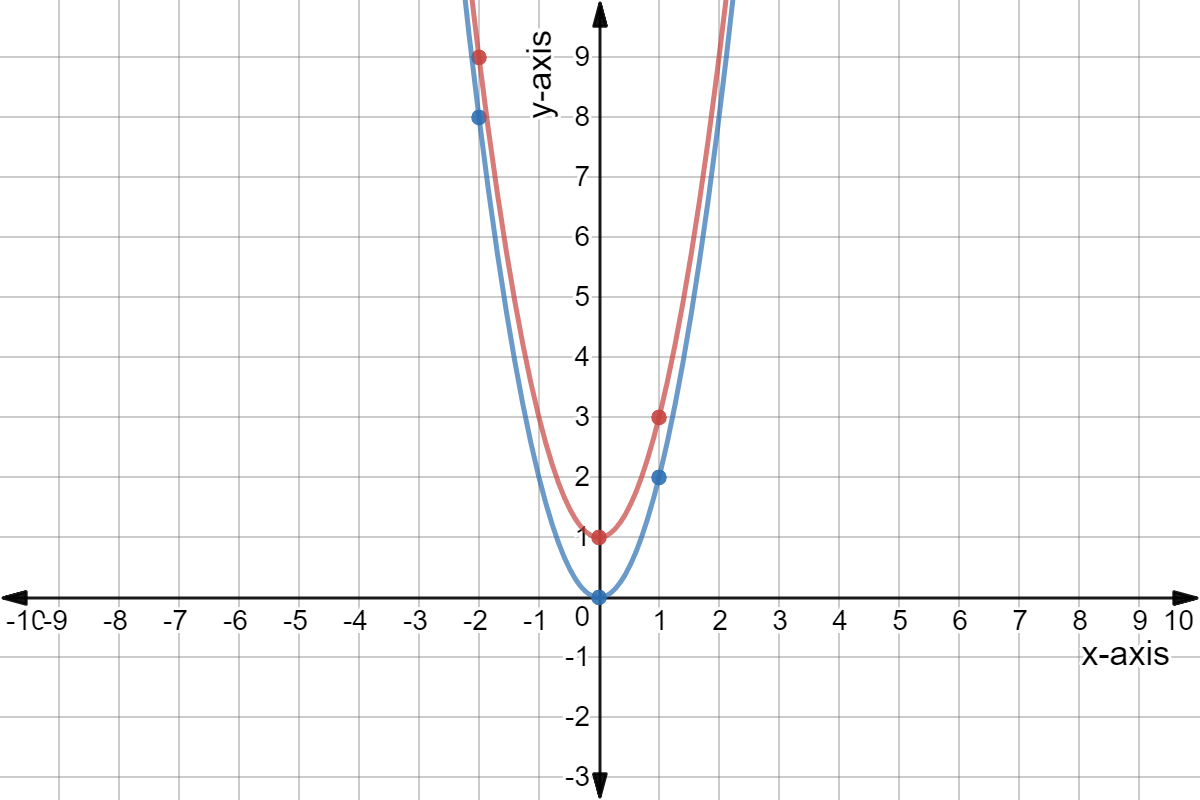



Quadratic Graph Example Y Ax C Expii



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola



Math 140 Lecture 28 Y Ax2 Bx C University Of San Diego



What Are The Coefficients A B And C Of The Parabola Y Ax 2 Bx C That Passes Through The Point 3 13 And Tangent To The Line 8x Y 15 At 2 1 Quora




Vertex Form How To Find The Equation Of A Parabola



How To Show That The Vertex Of The Parabola Math Y Ax 2 Bx C Math Can Be Expressed As Math B 2a C B 2 4a Math Quora
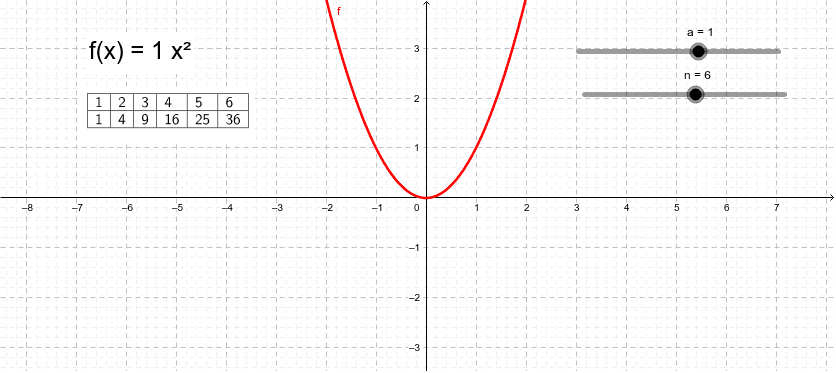



Parabola Y Ax 2 Geogebra




Algebra 2 Y 13 2 Parabolas Pages 1 4 Flip Pdf Download Fliphtml5



Search Q Quadratic Formula Tbm Isch



Exploring Parabolas Y Ax 2 Bx C



Http Facstaff Cbu Edu Wschrein Media M105 notes M105l80 Pdf




Find The Parabola Of The Form Y Ax 2 B Which Best Fits The Points 1 0 4 4 5 8 Mathematics Stack Exchange
/asGF.jpg)



Axis Of Symmetry Parabola
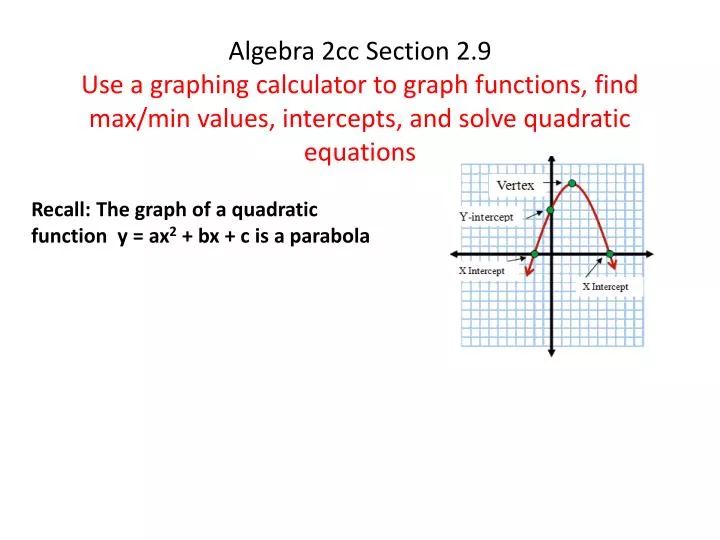



Ppt Recall The Graph Of A Quadratic Function Y Ax 2 Bx C Is A Parabola Powerpoint Presentation Id




Graphing Parabolas
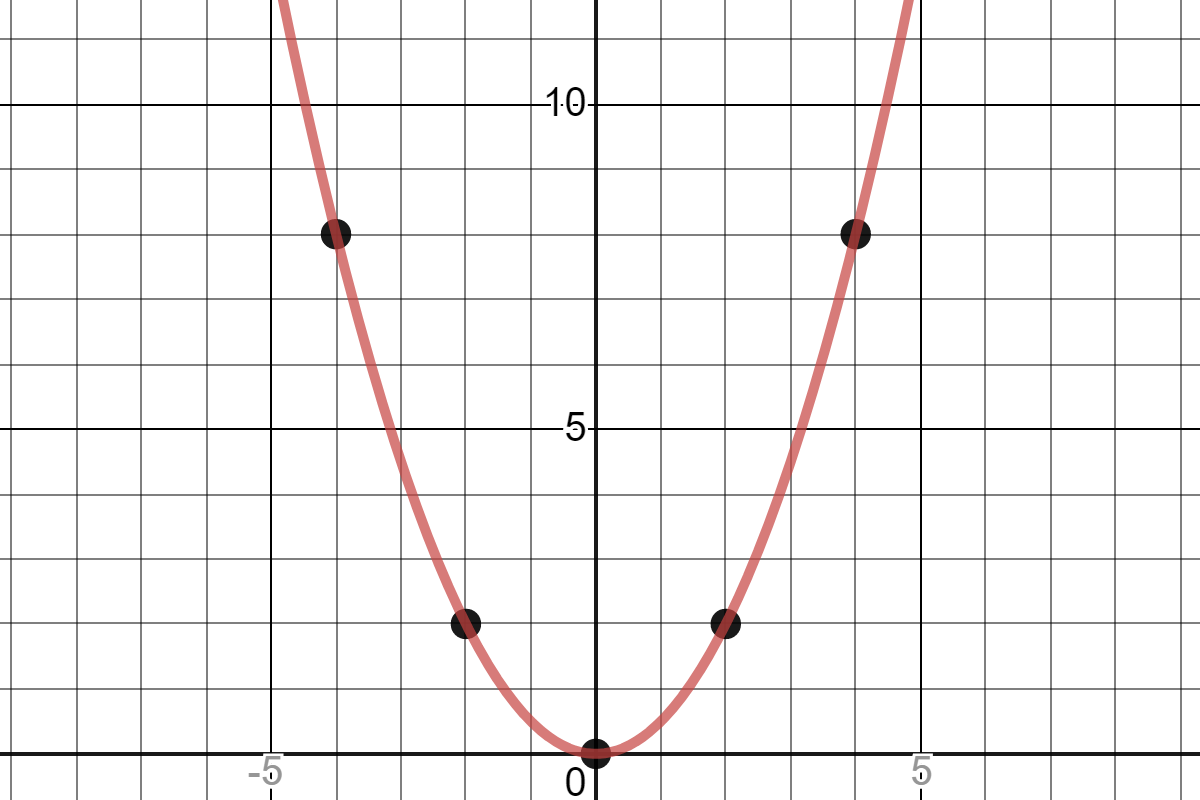



Quadratic Graph Example Y Ax Expii



Http Thunderbird Guhsdaz Org Common Pages Displayfile Aspx Itemid



To Investigate The Effect Of The Constants A B And C On The Graph Y Ax2 Bx C Gcse Maths Marked By Teachers Com
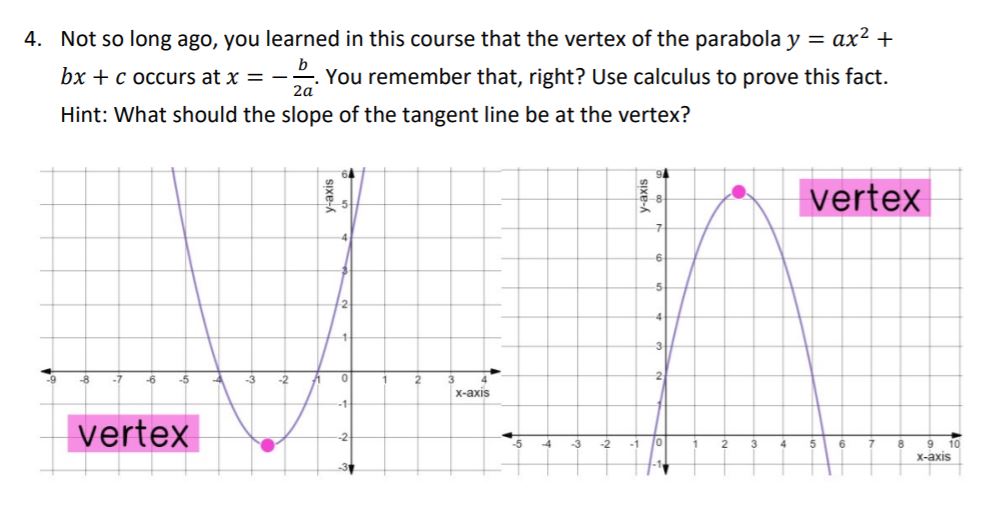



Answered Not So Long Ago You Learned In This Bartleby



Http Home Sandiego Edu Ekim Otherjunk Parabolavertex Pdf
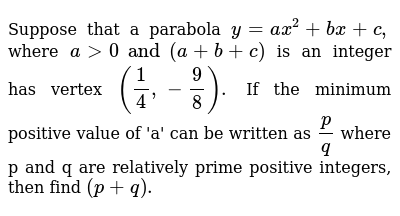



Suppose That A Parabola Y Ax 2 Bx C Where A 0 And A B




Quadratic Function



Math 140 Lecture 28 Y Ax2 Bx C University Of San Diego
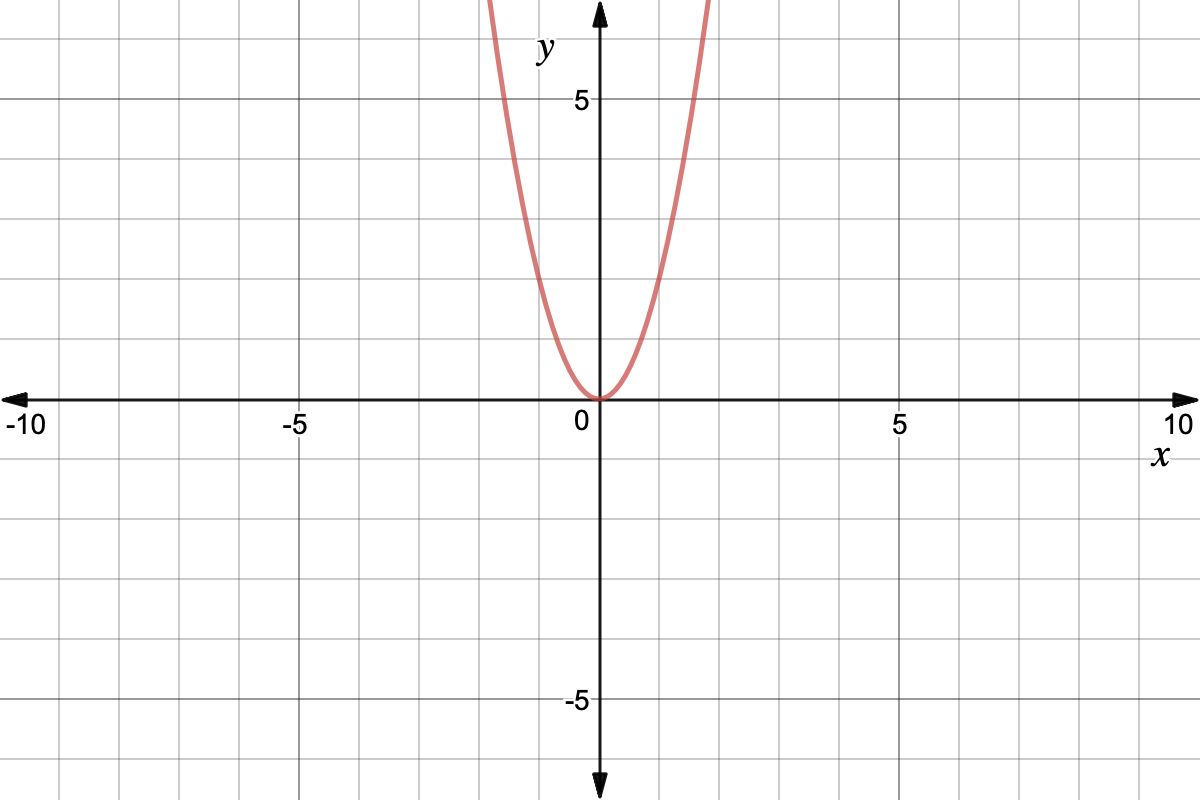



Quadratic Graph Example Y Ax Expii
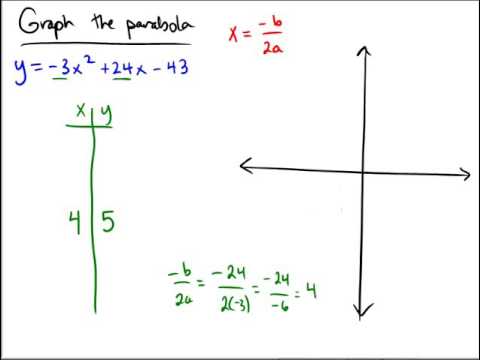



Graphing A Parabola Of The Form Y Ax 2 Bx C Integer Coefficients Youtube




The Parabola Y Ax 2 Bx C Is Graphed Below Find A B C The Grid Lines Are One Unit Brainly Com



Graphing Parabolas In The Form Y Ax 2 Youtube



A Tangent To A Quadratic
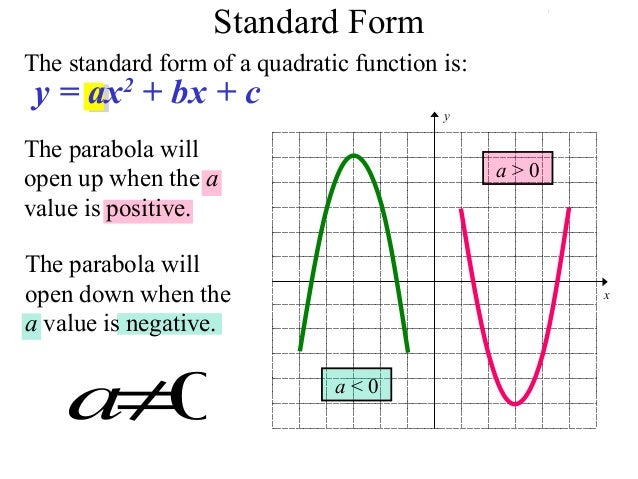



Graphing Quadratics



The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora



Transformations Of Equations Of Parabola Parametric Equations Of Parabola



View Question The Graph Of The Equation Y Ax 2 Bx C Where A B And C Are Constants Is A Parabola With Axis Of Symmetry X 3 Find B A



Examining The Parabola Assignment 2



Solution A Parabola Y Ax 2 Bx C Has Vertex 4 2 If 2 0 Is On The Parabola Then Find The Value Of Abc



Polynomials
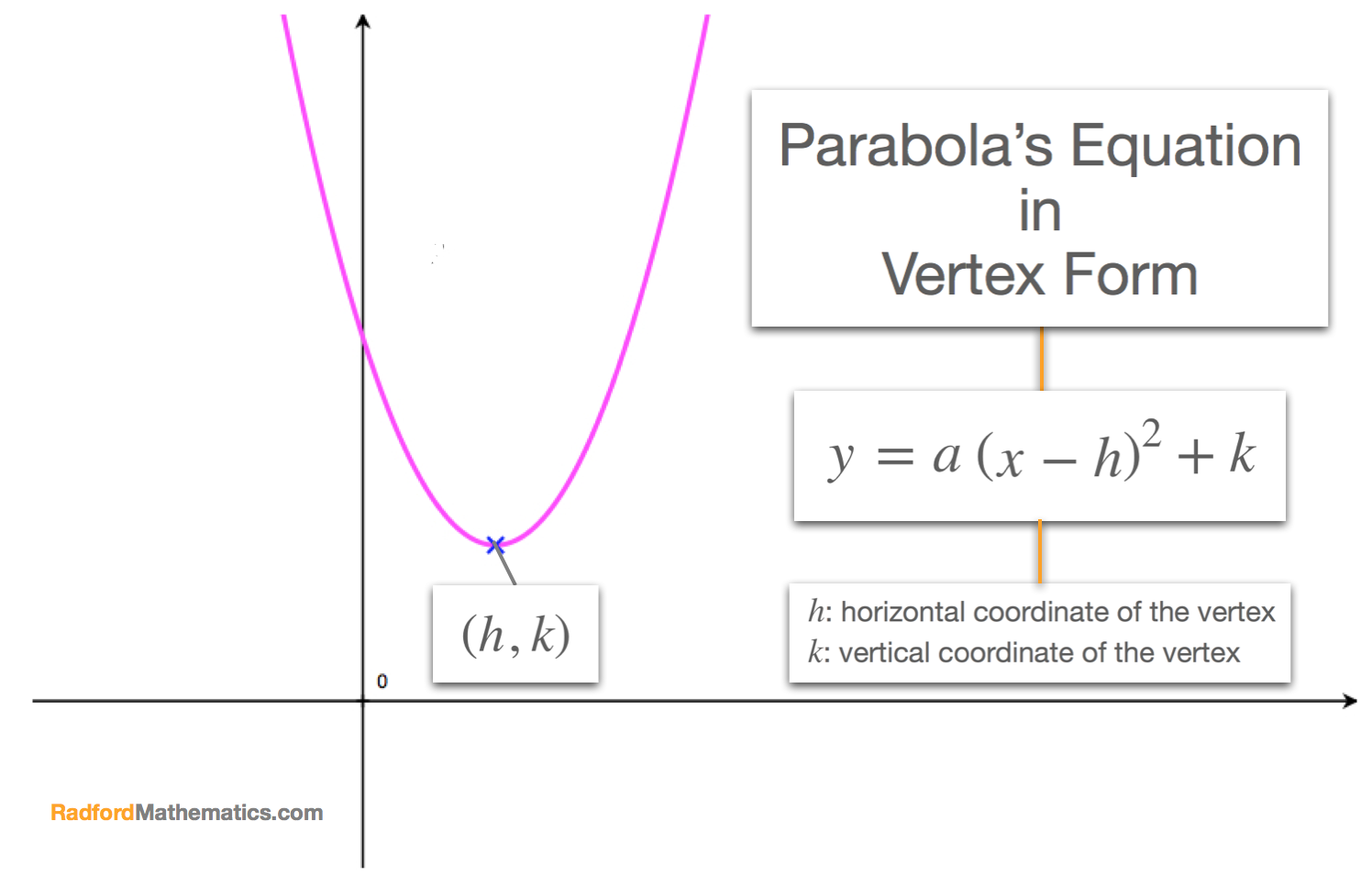



Vertex Form How To Find The Equation Of A Parabola



Unique Quadratic Equation In The Form Y Ax 2 Bx C
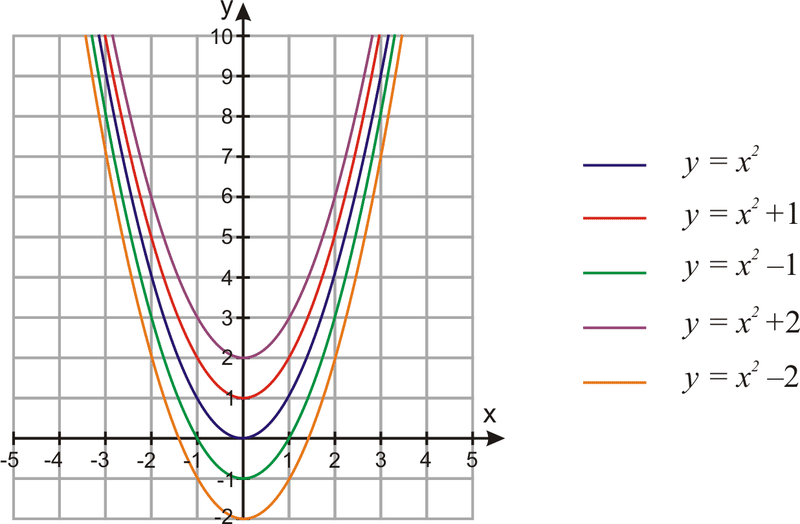



Vertical Shifts Of Quadratic Functions Ck 12 Foundation



The Department Of Mathematics Education J Wilson Emat 6680 Assignment 2 Quadratics By Hulya Kilic In This Assignment I First Constructed The Graphs Of Parabolas Having Standard Form Y Ax2 Bx C Here The Graphs Of The Parabolas That I Chose Then




The Equation For A Parabola Has The Form Y Ax 2 Bx C Where A B And C Are Constants Homeworklib
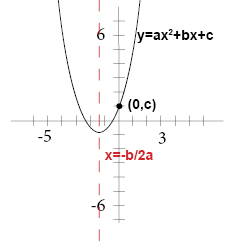



How Do You Graph F X 3x 2 4x 1 Socratic
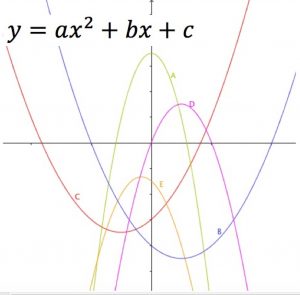



Quadratic Functions Aiming High Teacher Network
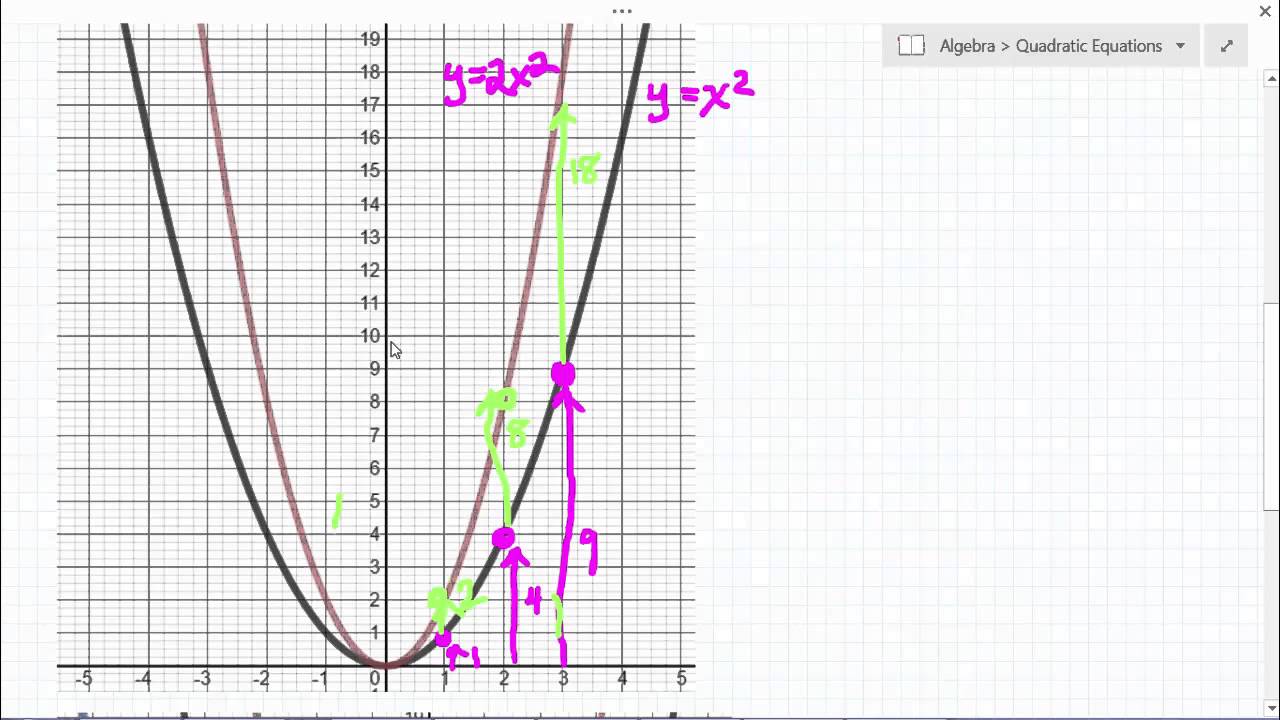



Graphing Parabola Y Ax 2 Youtube



All Elementary Mathematics Study Guide Functions And Graphs Elementary Functions And Their Graphs
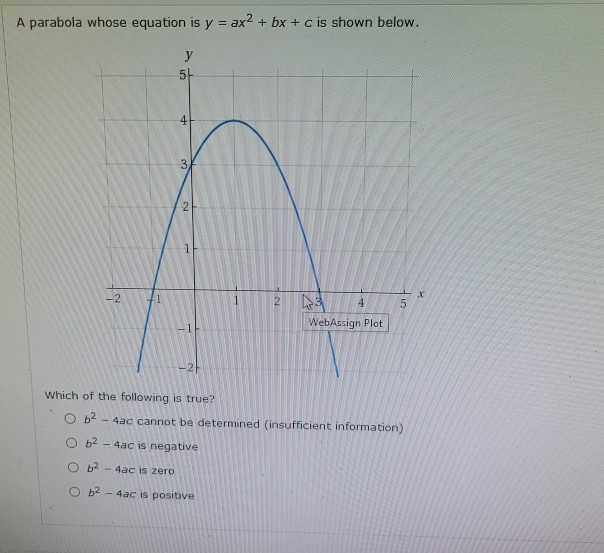



Solved A Parabola Whose Equation Is Y Ax2 Bx C Is S Chegg Com



1




The Graph Of Y Ax2 Bx C Is A Parabola That Opens U Gauthmath




Axis Of Symmetry Of A Parabola
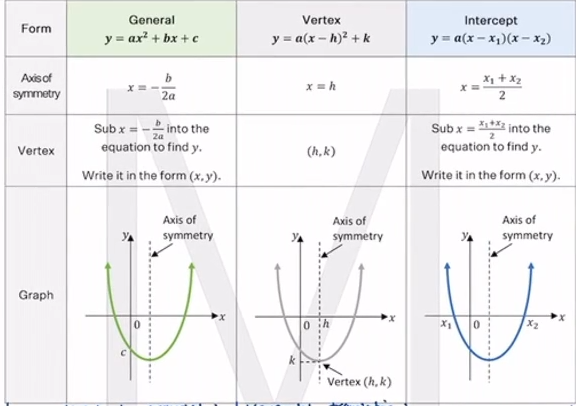



In A Nutshell Parabola Forms Adrian S Study Club



Vertex And Intercepts
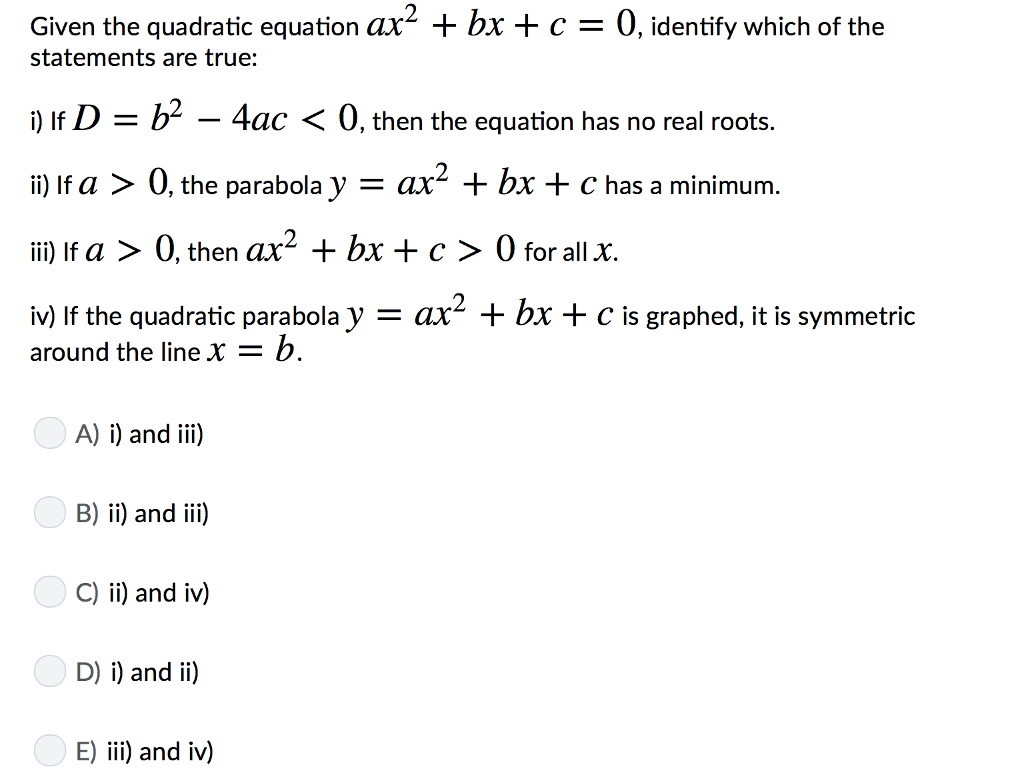



Given The Quadratic Equation Ax2 Bx C 0 Identify Chegg Com
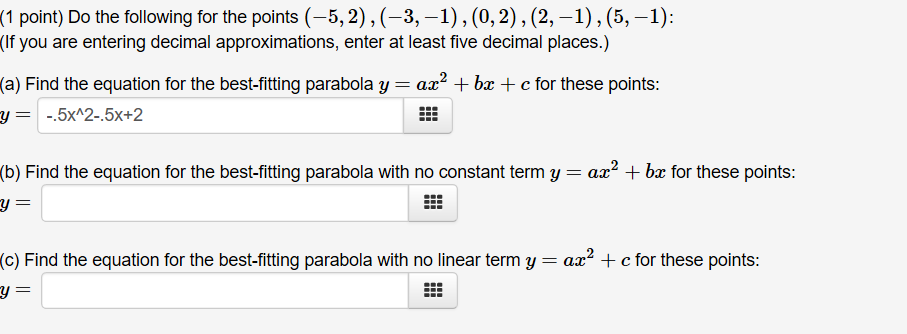



Find The Equation For The Best Fitting Parabola Chegg Com
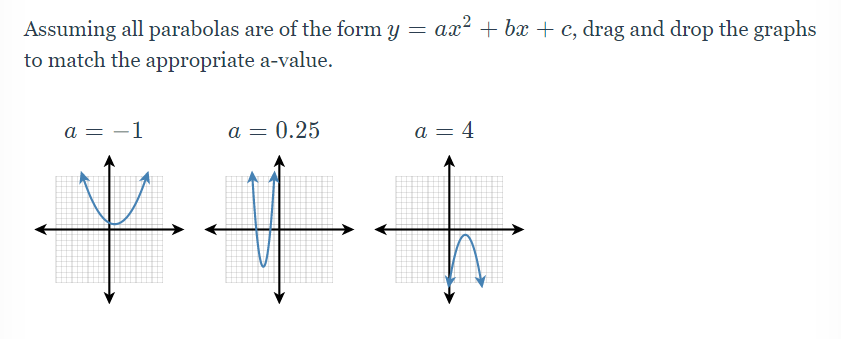



Answered Assuming All Parabolas Are Of The Form Bartleby
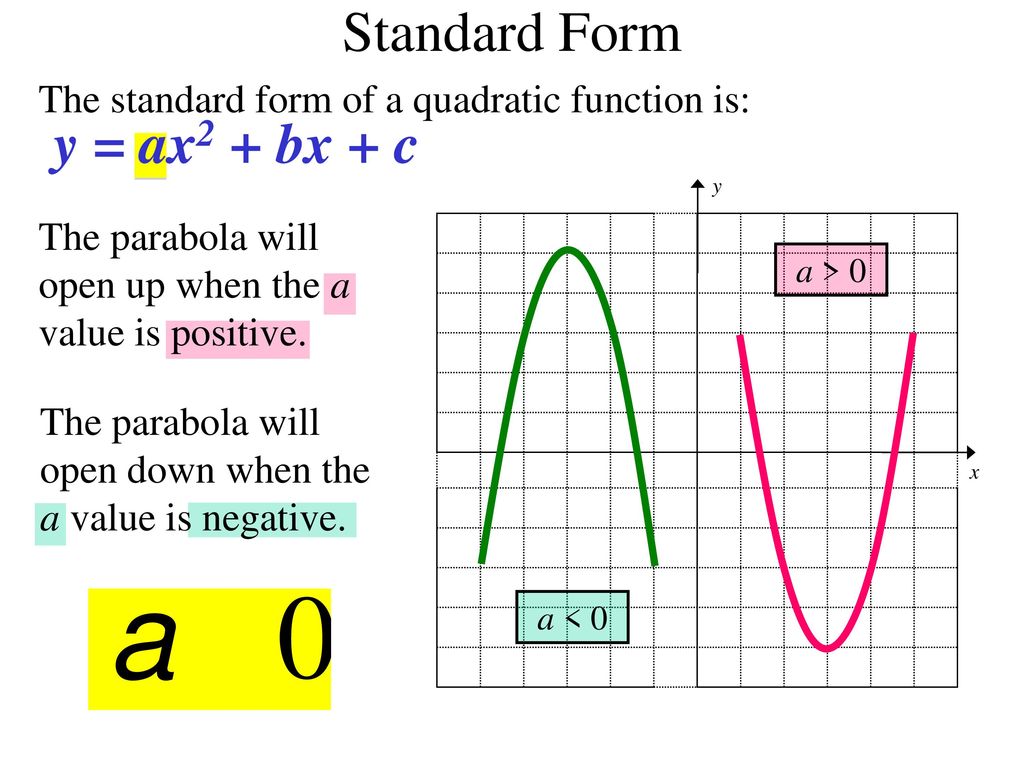



Y Ax2 Bx C Quadratic Function Quadratic Term Linear Term Ppt Download



Find The Parabola With Equation Y Ax 2 Bx Whose Tangent Line At 2 4 Has Equation Y 8x Brainly Com



Show That Y Ax 2 Bx C A 0 Represents A Parabola And Find Its Vertex Focus Directrix And Latus Rectum Sarthaks Econnect Largest Online Education Community



Sat Math Grid Ins Question 97 Answer And Explanation Cracksat Net



Quadratics



Examining The Parabola Assignment 2




This Is What The Problem Says Assuming All Parabolas Are Of The Form Y Ax 2 Bx C Drag And Drop The Brainly Com



0 件のコメント:
コメントを投稿