Parabola y=4x-x^2 308102-Parabola y=x^2-4x-12

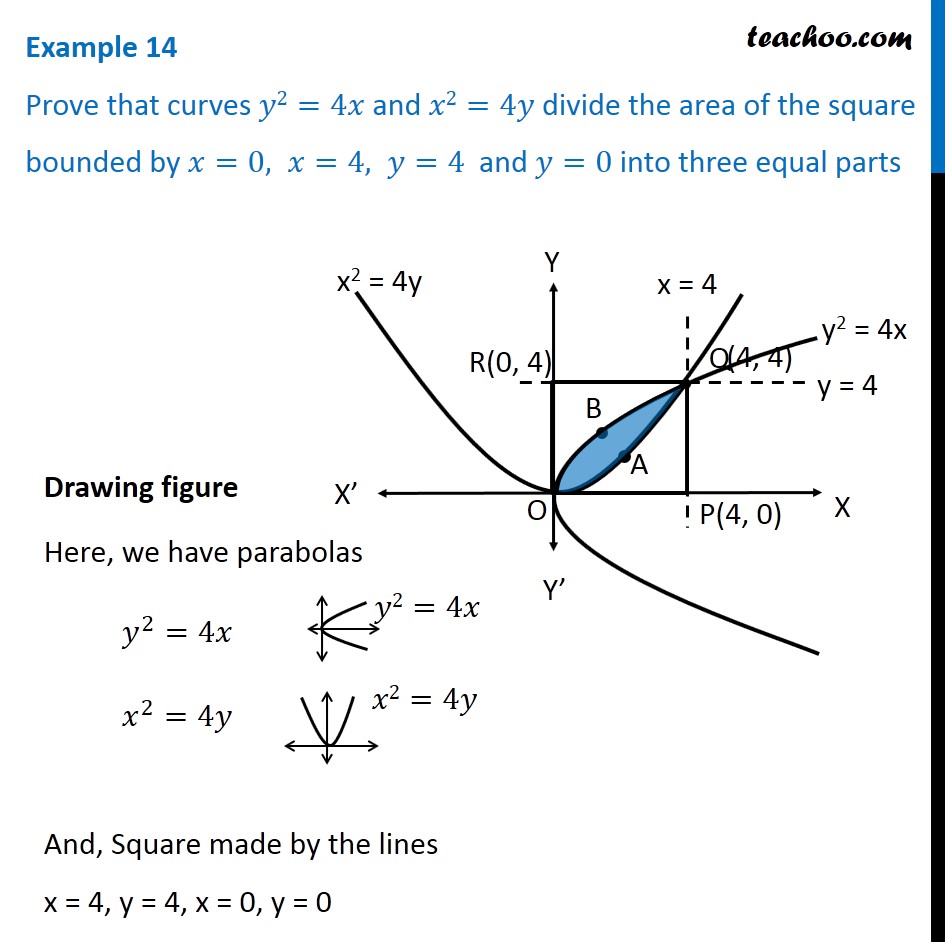
194 Introducción al cálculo integral 21) 2Calcular el área de la figura comprendida entre las parábolas y = x, 2 x2 y = y la recta y = 2x Solución A= 4 22) Hallar el área de la figura limitada por la curva y = x3, la recta y = 8 y el eje OY Solución A=12 23) Hallar el área del dominio comprendido entre las parábolas y2 = 2px, x2 = 2py Solución 2A = − 1, b = − 4, c = − 1 a = 1, b = 4, c = 1 Consider the vertex form of a parabola a ( x d) 2 e a ( x d) 2 e Substitute the values of a a and b b into the formula d = b 2 a d = b 2 a d = − 4 2 ( − 1) d = 4 2 ( 1) Simplify the right sideThe Area Bounded by the Parabola X = 4 − Y2 and Yaxis, in Square Units, is CBSE CBSE (Arts) Class 12 Question Papers 17 Textbook Solutions Important Solutions 24 Question Bank Solutions Concept Notes & Videos 532 Time Tables 18 Syllabus

How To Find The Volume Of The Solid Generated By Revolving The Region Bounded By Math Y 4x X 2 Math Math Y X Math About The Y Axis Quora

Parabola y=x^2-4x-12

Parabola y=x^2-4x-12-Parabola is y2 = xand line is xy = 2Solving bothx = 2−y⇒ y2 = x⇒ y2 = 2−y⇒ y2 y −2= 0⇒ y2 2y−y−2 = 0⇒ y(y2)−1(y2)= 0⇒ (y−1)(y2)= 0⇒ y = 1,−2Area included between line and parabola is the area of shaded region∫ y1 y2 xdy = ∫ −21 ((2−y)−y2)dy= 2y− 2y2 − 3y3 −21 = 2− 21 − 31 −(−4−2INTEGRALES DOBLES SOBRE REGIONES GENERALES 6 En la integral doble ZZ D f(x,y)dxdy, colocar los l´ımites de integraci´on en ambos ordenes, para los siguientes recintos

Find The X Intercepts Of Thr Following Parabola Y 4x 2 8x 12 Brainly Com

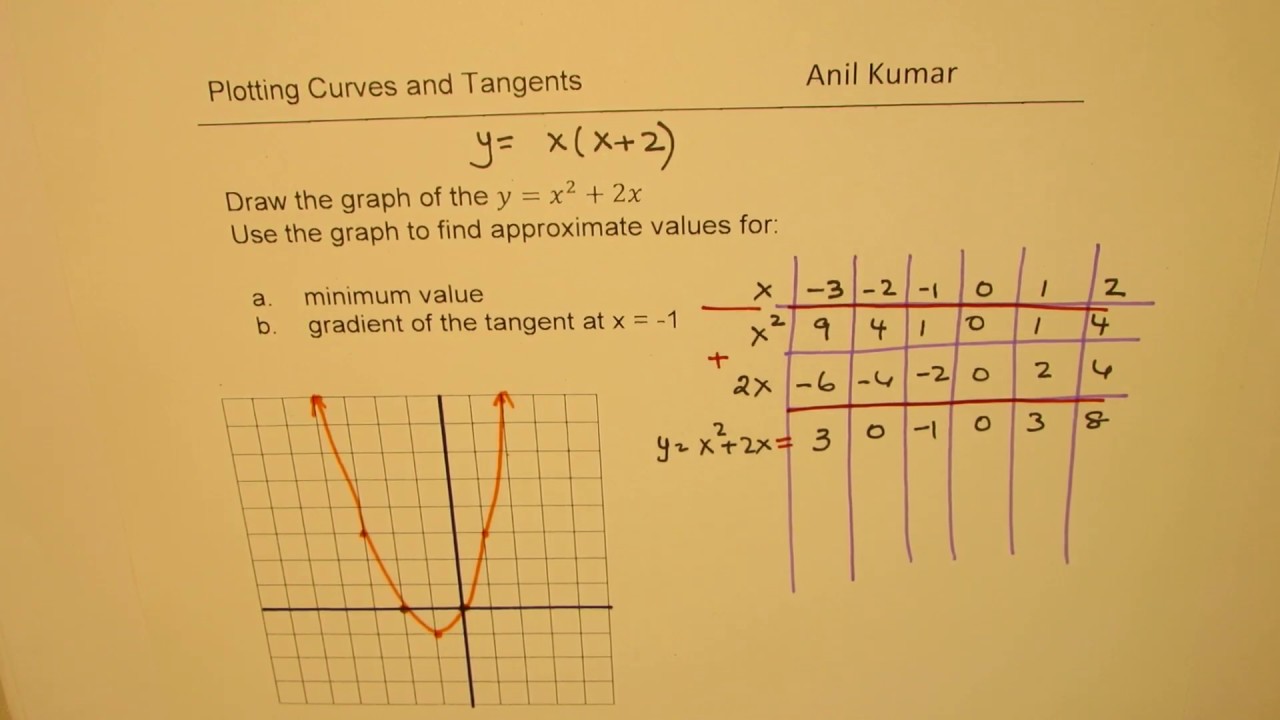
Questa è l'equazione di una parabola con il vertice nell'origine O, con l'asse di simmetria coincidente con l'asse y e con il fuoco nel punto di coordinate F ( 0, 1 4 a) con la retta direttrice che ha equazione y = 1 4 a se a > 0 la parabola è contenuta nel semipiano superiore delle ordinate positive o nulle, dunque si dice che essa ha laPor ejemplo, esta gráfica corresponde a la parábola y = 4x x 2 con x tomando valores desde 0 hasta 4 A partir de los punto marcados, y trazando perpendiculares al eje OX, obtenemos una serie de trapecios y triángulos , cuya suma de áreas se aproximará al área bajo la curvaComplete the square for y 2 4 y 2 4 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 1 4, b = 0, c = 0 a = 1 4, b = 0, c = 0 Consider the vertex form of a parabola a ( x d) 2 e a ( x d) 2 e

 Find the centroid of the region in the first quadrant bounded by the xaxis, the parabola y^2 = 2x, and the line x y = 4 I've graphed the function, and it looks like a triangle with one side curved (the parabola) I'm not quite Maths find the area of the region bounded by the parabola y^2= 16x and its latus rectum Pembahasan Cara 1 Menggunakan Integral Daerah yang diarsir dibatasi oleh dua kurva parabola, yaitu y = x 2 − 2 x dan y = 6 x − x 2 Perhatikan bahwa dari selang ( 0, 4), kurva y = 6 x − x 2 selalu berada di atas kurva y = x 2 − 2 x Dengan demikian, luasnya dapat ditentukan dengan menggunakan integral tentu berikut Aplikasi integral 1 PENGGUNAAN INTEGRAL 1 Pengertian Luasan Tujuannya adalah mencari luas daerah yang diarsir yang dibatasi oleh kurva y=f (x), sumbu x dan ordinat di x=a dan x=b Misalkan P (x,y) adalah sebuah titik pada kurva y=f (x) dan misalkan Ax menyatakan luas dibawah kurva yang dibatasinya diukur dari sebuah titik di kiri kurva Jika

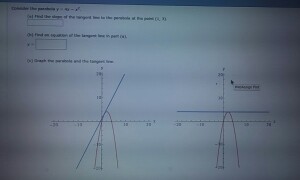
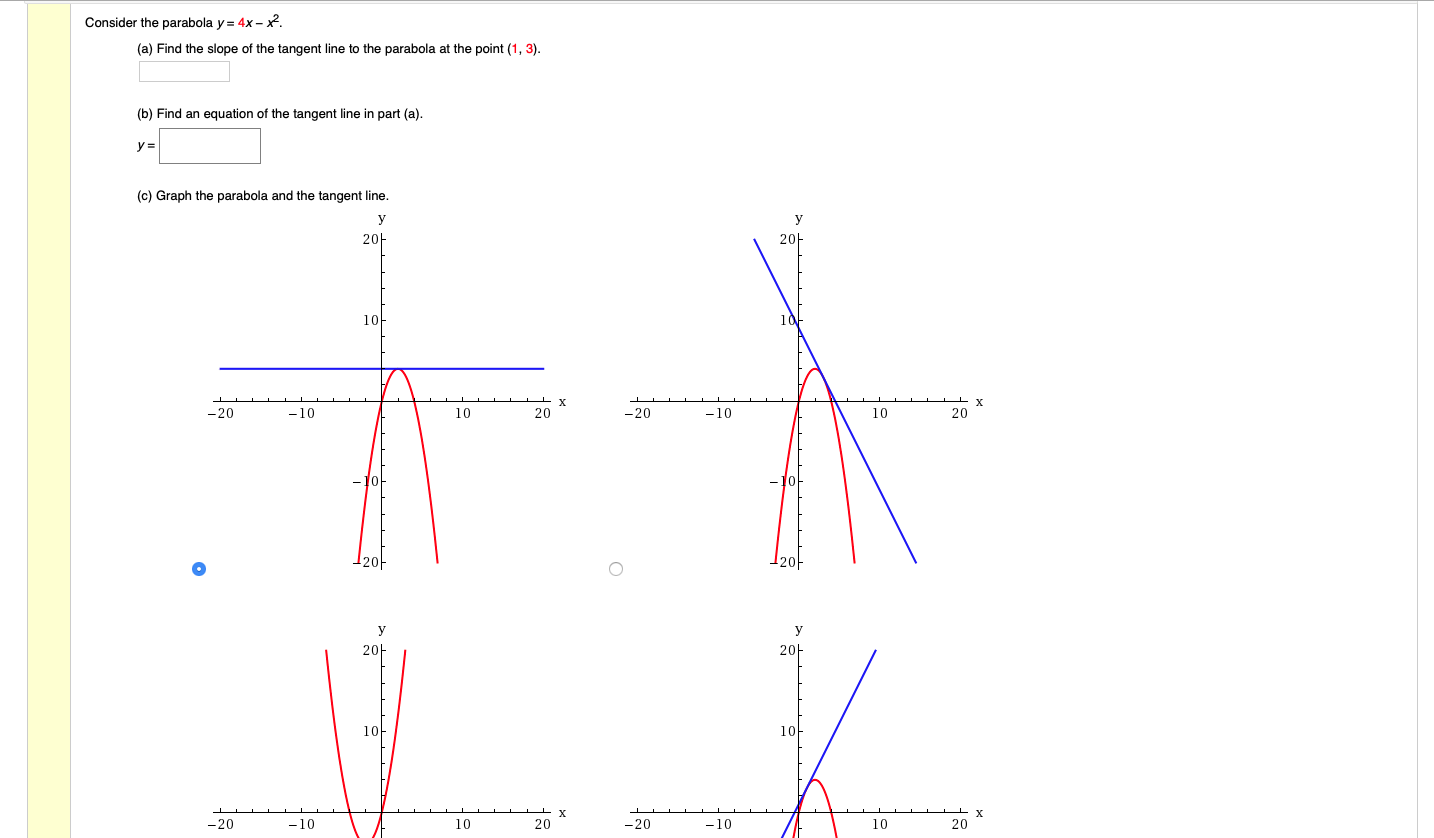
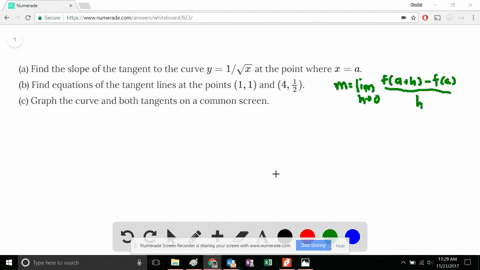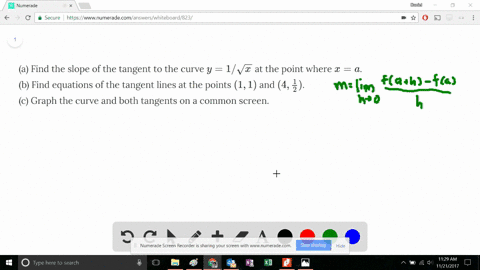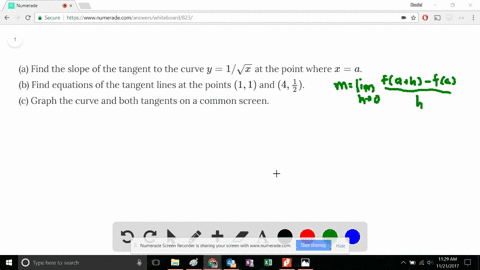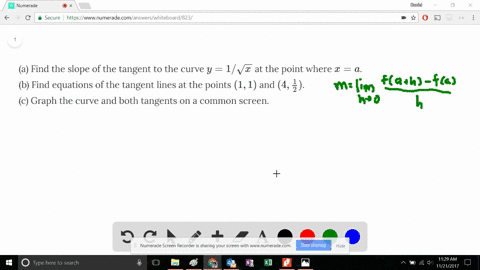
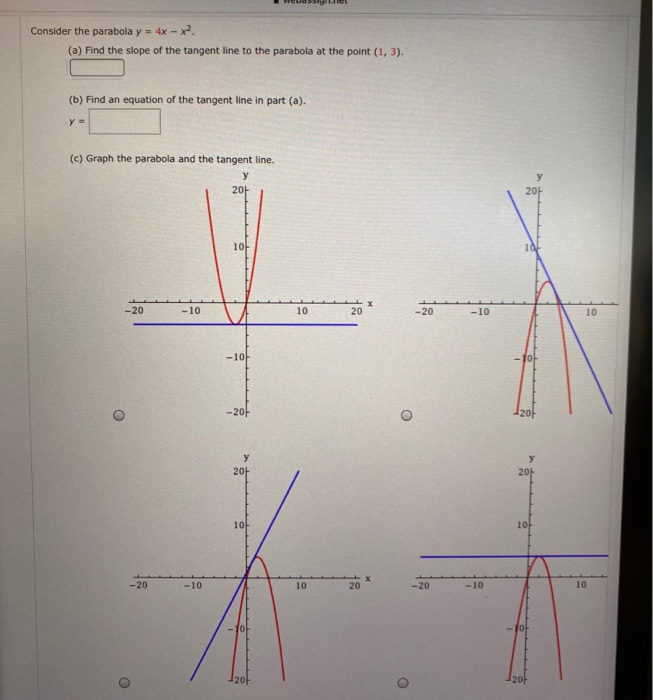
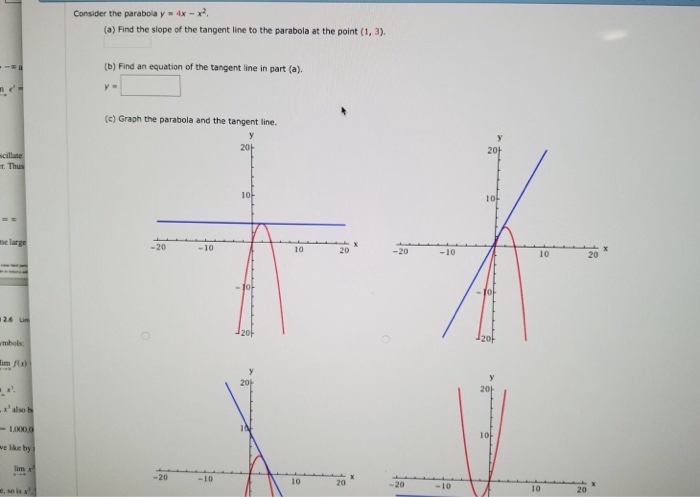
Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeConsider the parabola y = 4x x^2 (a) Find the slope of the tangent line to the parabola at the point (1, 3) _____ (b) Find an equation of the tangent line in part (a)Since the parabola opens to the left, then the focus is 1/4 units to the left of the vertex I can see from the equation above that the vertex is at (h, k) = (0, –5), so then the focus must be at (–1/4, –5) The parabola is sideways, so the axis of symmetry is, too

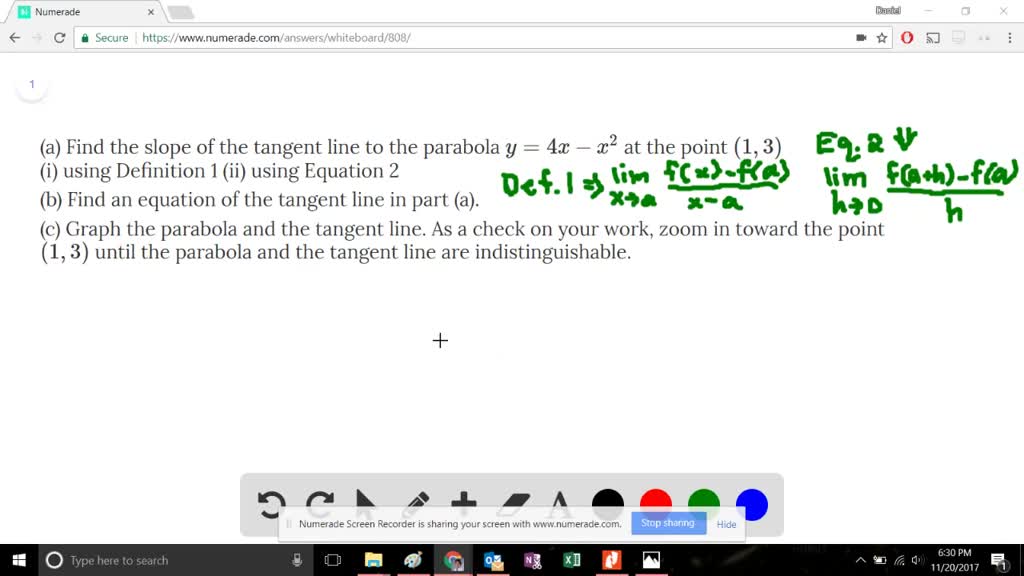
Solved A Find The Slope Of The Tangent Line To

Compute The Volume Of The Solid Generated By Revolving About The X Axis The Region Bounded By The Line X 2y 0 And The Parabola Y 2 4x Study Com

To find a parabola equation, we need to have the information of at least 1 Two points, if one of the points is the vertex 2 Three points, if there are no vertex point given We obtain theSe determina vertice, foco y recta directriz de la parabola Se realiza un boceto Se muestra la ecuacion de una parabola en su forma reducida (x2)^2=8(y4)2 Soluciones Aplicaciones de I definida Ejercicio nº 1 Halla el área del recinto delimitado por la función 𝒇𝒙= 𝒙 − 𝒙 y el eje X Solución Puntos de corte con el eje X Área total 4 4 8 u2 La gráfica no es necesaria, pero la incluimos para visualizar el resultado

Solution What Is The Area Bounded By The Curve Y 2 4x And X

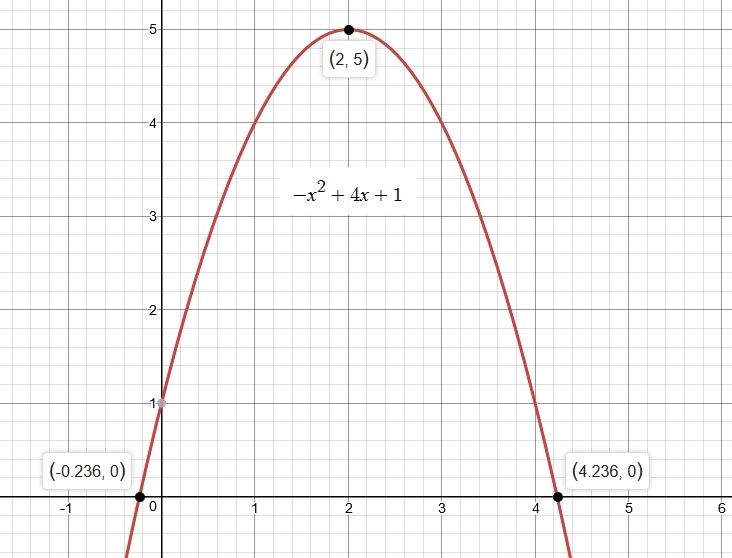
How Do You Find The Max Or Minimum Of F X 4x X 2 1 Socratic

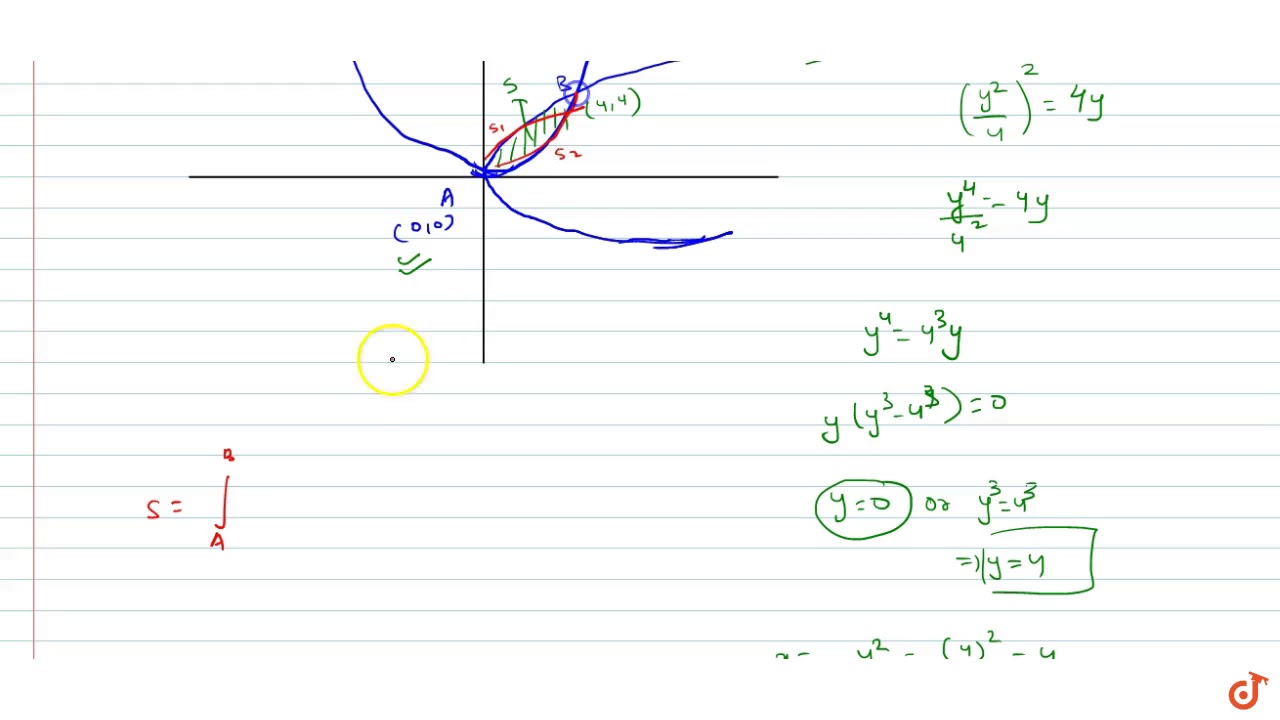
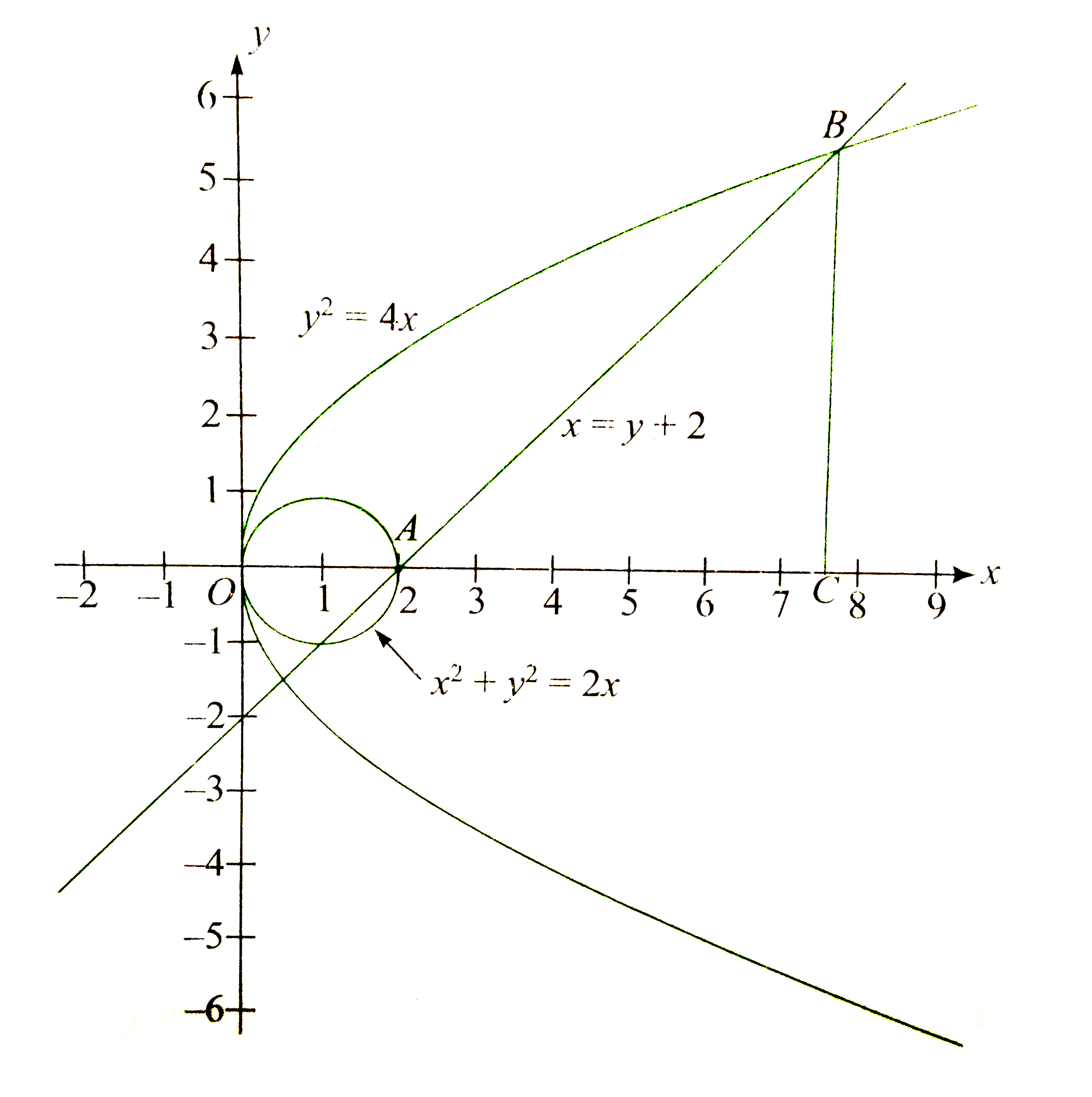
 The parabolas y^2 = 4x and x^2 = 4y divide the square region bounded by the lines x = 4, y = 4 0 votes 412k views asked in Mathematics by Samantha (3k points) The parabolas y2 = 4x and x2 = 4y divide the square region bounded by the lines x = 4, y = 4 and the coordinate axes If S1, S2 and S3 are respectively the areas of theseThe equation of parabola isy2 = x (1)The equation of line isx y = 2 (2)From (2), y = 2 x (3)Putting this value of y in (1), we get,(2 x)2 = xor x2 4 x 4 = x or x2 5 x 4 = 0 ∴ (x 1) (x 4) = 0∴ x = 1, 4∴ from (3), y = 1, 2∴ parabola (1) and line (2) intersect in the points A (1, 1), B (4, 1)Also line (2) meets xaxis in C (2,0)Required area is shadedAreaAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators

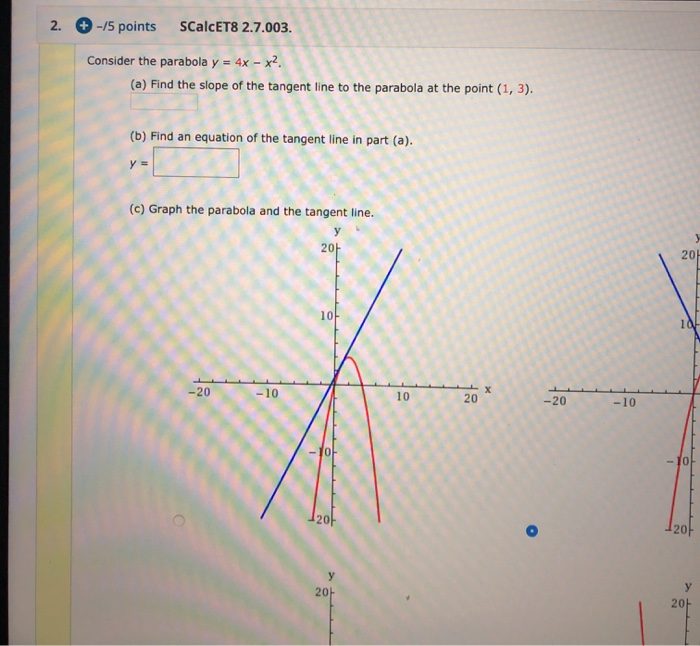
Solved Scalcet8 2 7 003 2 5 Points Consider The Parab Chegg Com

Solution How Many Times Does The Parabola Y 4x 2 12x 9 Intersect The X Axis

63 Cálculo II – Profa Adriana Cherri _____ Notas de aula baseadas no livro Cálculo v1– James Stewart e Cálculo A – Flemming e Gonçalves Se a velocidade média for calculada em intervalos cada vez menores a, ah, fazemos h → 0 Definimos velocidade instantânea v(a) no instante t = a como o limite das velocidadesX – axis (1) And y = 4x – x2 (2) ⇒ y 4 = – (x2 – 4x – 4) (adding 4 on both sides) ⇒ – (y 4) = (x – 2)2 equation (2) represents a downward parabola with vertex at (2,4) and passing through (0, 0) and (4, 0) on the x – axis, A rough sketch is given asZ u Find the volume generated by revolving the area cut off from the parabola y = 4x — x2 by the x axis about the line y = 6 We divide the area vertically (Fig 4110) The solid generated by revohnng the approximating rectangle about the line y = 6 is a washer whose volume is Ax— qr(6 — Ax The required volume is then Fig 4113 (6)2

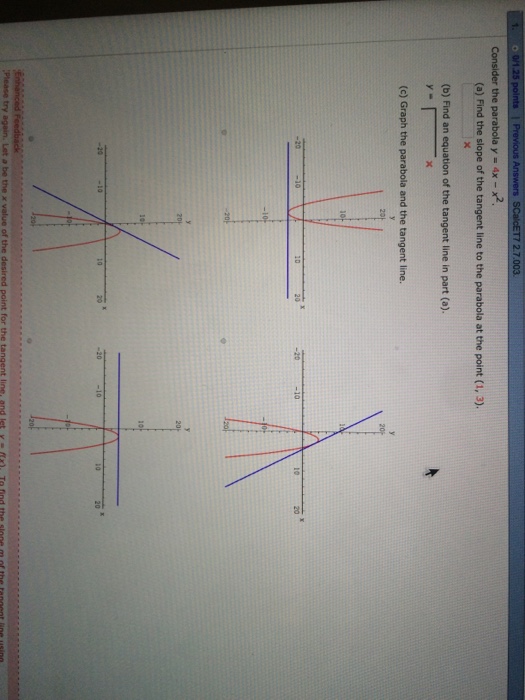
Solved Consider The Parabola Y 4x X 2 A Find The S Chegg Com

Solution Find The Coordinates Of The Turning Point Of The Curve Y 6 4x X 2 By Expressing This Equation In The Form A X B 2 And Determine The Nature Of This Turnin

Help with line integral over parabola Hot Network Questions Exodus 4 order prohibiting making idols in the likeness heavenly aspects w/ Tabernacle(Exodus 2518Resolvemos problemas de matemáticas respondiendo a preguntas sobre tus deberes de álgebra, geometría, trigonometría, cálculo diferencial y estadísticas con explicaciones paso a paso, como un tutor de matemáticas The area bounded by the parabola ` y = 4x x^ (2)` and Xaxis is Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting

The Region Between Y 4x X 2 And The X Axis Is Rotated Around The Y 6 Line How Can I Find The Volume Of The Object Formed Quora

Exploration Of Parabolas

How do I calculate the arc length in the range 0,4 of the parabola y = 4xx^2?The equation of the parabola is y = 4 – x 2 ∴ x 2 = 4 – y, ie (x – 0) 2 = – (y – 4) It has vertex at P(0, 4) For points of intersection of the parabola with Xaxis, we put y = 0 in its equation ∴ 0 = 4 – x 2 ∴ x 2 = 4 ∴ x = ± 2 ∴ the parabola intersect the Xaxis atThe given equation is y = 4x−x2 y′ = 4−2x y = 4 x − x 2 y ′ = 4 − 2 x The slope of the tangent at (1,3) is = 4−2×1= 4−2= 2 4 − 2 × 1 = 4 − 2 = 2 Now we are given that

Find The Area Of The Region Bounded By Y 4x 2 And X 0 Y 1 Y 4 In First Quadrant Brainly In

Ex 21 1 Q4 Find The Area Lying Above The X Axis And Under The Parabola Y 4x X 2

Two numbers r and s sum up to 4 exactly when the average of the two numbers is \frac{1}{2}*4 = 2 You can also see that the midpoint of r and s corresponds to the axis of symmetry of the parabola represented by the quadratic equation y=x^2BxC The values of r and s are equidistant from the center by an unknown quantity uAdd − 2 2 and 4 4 Plug in the slope of the tangent line and the x x and y y values of the point into the point slope formula y−y1 = m(x−x1) y y 1 = m ( x x 1) Simplify Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yinterceptThe effects of a and q on f(x) = ax2 q For q > 0, f(x) is shifted vertically upwards by q units The turning point of f(x) is above the x axis For q < 0, f(x) is shifted vertically downwards by q units The turning point of f(x) is below the x axis q is also the y intercept of the parabola

Solution There Are Two Tangent Line To The Curve Y 4x X 2 That Pass Through The Point 2 5 Find The Equations Of These Two Lines And Make A Sketch To Verify Your Results

All Answer Sample Test 4 1575 Calculus Ii 1 The Region Bounded By The Parabola Y 4x X And The X Axis Is Revolved About Thex Axis Find The Volume Of The Solid Write

 You prepare a chart of x and y values and plot the points x= y^2 4y 3 Note that x is the dependent variable and y is the independent variable Step 1 Prepare a chart Try an interval from y = 5 to y = 5, and calculate the corresponding values of x Step 2 Plot these points Step 3 Add points to make the plot symmetrical We need some extra points on the top portion of theLa parabola di equazione y a b C d ha concavità rivolta verso il basso ha fuoco di ordinata passa per il punto P — 1;— ha apertura maggiore rispetto alla parabola di equazione y = Determina per quali valori di a la parabola di equazione y = (2a — 4)x2 ha concavità rivolta verso l'alto e disegna la parabola che si ottiene per a = aStack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange

What Is The Volume Of The Solid Bounded By The Parabola Y 4x 2 And The Lines X 0 And Y 16 By Revolving About The Line Y 2 Quora

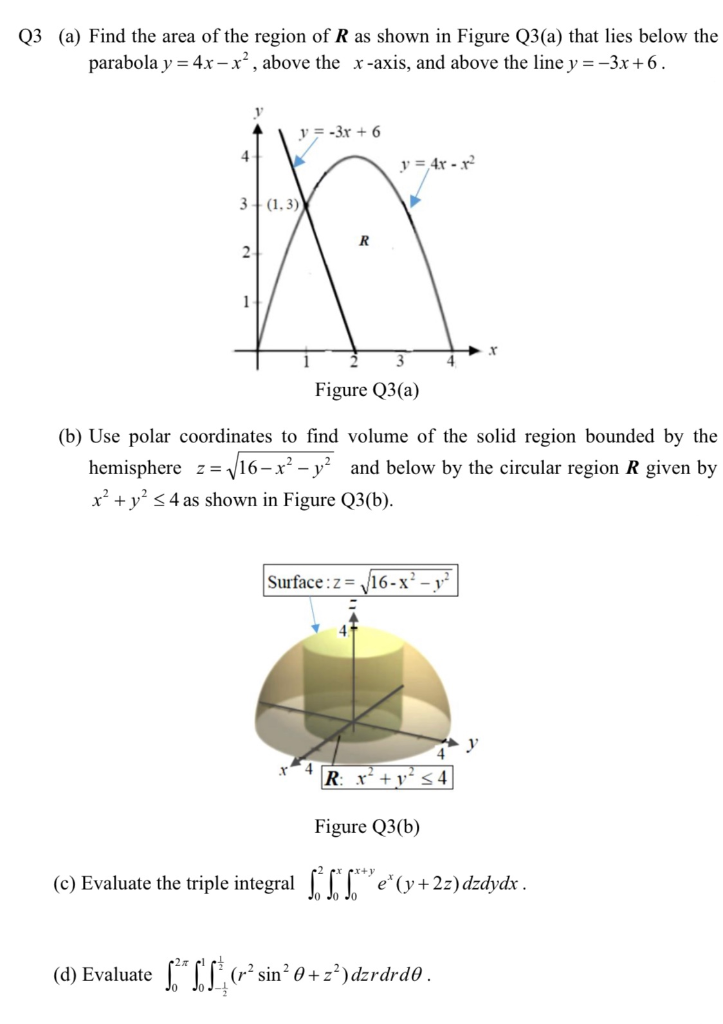
Q3 A Find The Area Of The Region Of R As Shown In Chegg Com

 Find the area of the region in the first quadrant bounded by the parabola y = 4x^2 and the lines x = 0, y = 1 and y = 4 asked May 4 in Definite Integrals by Yajna ( 299k points) area of bounded regionsSolved The Region Bounded By The Parabola Y 4x X 2 An Chegg Com For more information and source, see on this link https//wwwcheggcom/homeworkhelp/questionsandanswers/regionboundedparabolay4xx2axisrevolvedxaxisfindvolumesolidwriteanswertermThe best videos and questions to learn about Vertex Form of a Quadratic Equation Get smarter on Socratic

Math1 2

How To Find The Volume Of The Solid Generated By Revolving The Region Bounded By Math Y 4x X 2 Math Math Y X Math About The Y Axis Quora

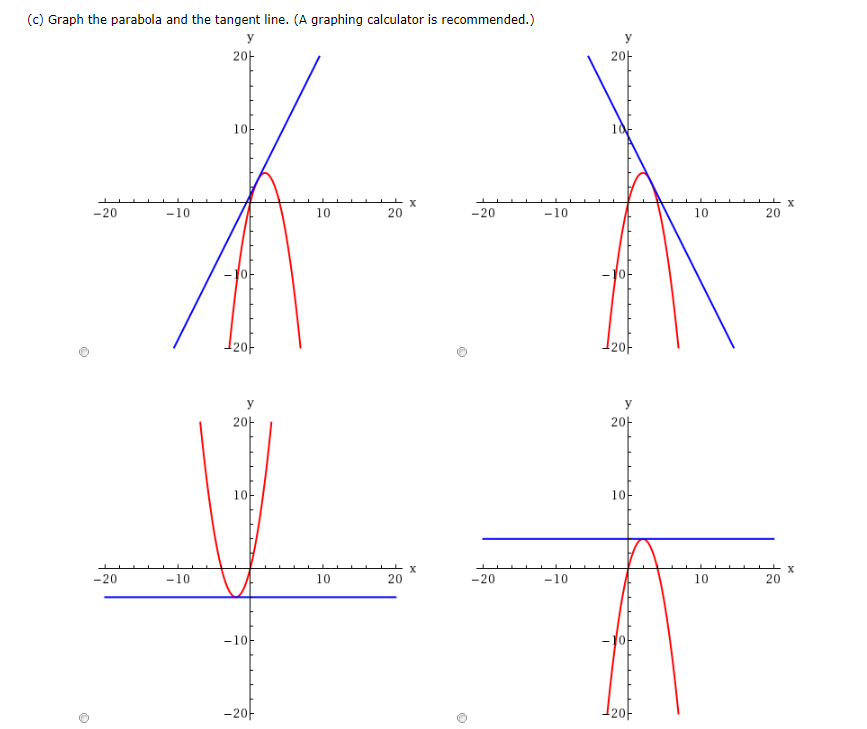
Graph the parabola y = x^2 4x 1 Graph the parabola y = x^2 4x 1 Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restartingCálculo del área entre una parábola y el eje x Se explica qué debe hacerse como primer paso, cómo es la función de acuerdo a la información que se dan, se eConsider the parabola y = 4x x^2 (a) Find the slope of the tangent line to the parabola at the point (1,3) (b) Find the equation of the tangent line in part (a) y = (c) Graph the parabola

Sketch The Region R That Lies Below The Parabola Y 4x X 2 Above The X Axis And Above The Line Y 3x 6 Find The Area Of This Region R Study Com

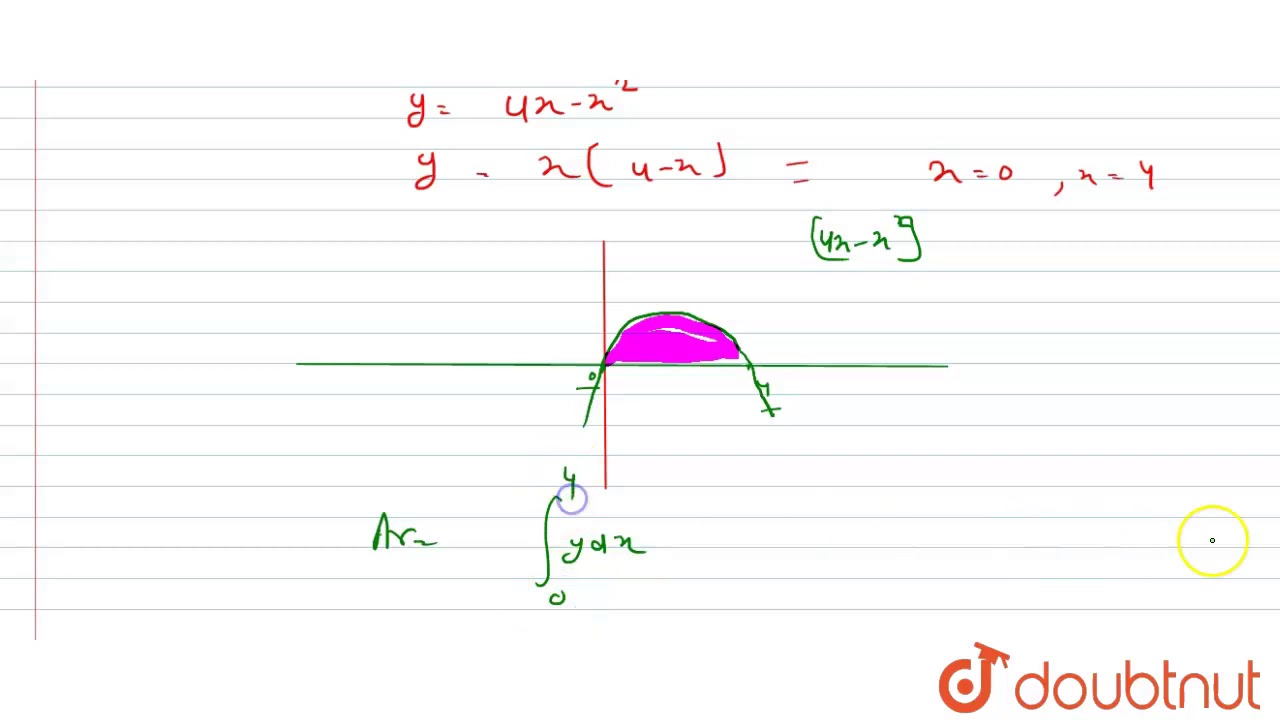
The Area Bounded By The Curve Y 4x X 2 And X Axis Is A 30 7 Sq Units B 31 7 Sq Units Youtube

E = 4 e = 4 e = 4 e = 4 Substitute the values of a a, d d, and e e into the vertex form a ( x d) 2 e a ( x d) 2 e − ( x − 2) 2 4 ( x 2) 2 4 − ( x − 2) 2 4 ( x 2) 2 4 Set y y equal to the new right side y = − ( x − 2) 2 4 y = ( x 2) 2 4 y = − ( x − 2) 2 4 y = ( x 2) 2 4V= (π)∫y^2dx, within limit x = 0 to a = (π)∫(4ax)dx, limits 0 to a = 4Find the area lying above the xaxis and under the parabola y = 4x − x 2 Advertisement Remove all ads Solution Show Solution \\text{ The equation }y = 4x x^2\text{ represents a parabola opening downwards and cutting the }x \text{axis at O(0, 0) and }B(4, 0)\

Write The Definite Integral That Represents The Area Of The Region Enclosed By The Parabola Y 4x X 2 And The X Axis Then Evaluate The Integral Study Com

Find The Area Of The Region Bounded By The Parabola Y 2 4x The X Axis And The Lines X 1 And X 4 Sarthaks Econnect Largest Online Education Community

Ad by Wondrium Never stop learning Stream your passions, your "aha" feelings, your mindblown moments Try 14 days of Wondrium on us Sign Up 3 Answers Enrico Gregorio, Associate professor in Algebra Find the area of the region included between the parabola y^2 = 4ax and x^2 = 4ay Where a > 0 asked in Mathematics by Nakul01 (369k points) bseb model set;Volume V of the solid generated by revolving the area cut off by latus rectum (x = a) of the parabola y^2 = 4ax, about its axis, which is x axis, is given by the formula;

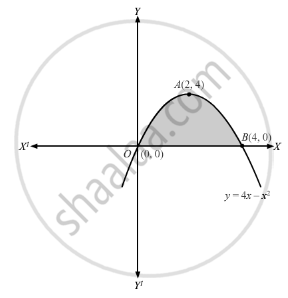
Find The Area Lying Above The X Axis And Under The Parabola Y 4x X2 Mathematics Shaalaa Com

Grafica De La Parabola Y 4x X2 Donde X Es 2 1 0 1 2 3 4 Brainly Lat

Class12 1 vote 1 answer Find the area of the region included between the parabolas y^2 = 4ax and x^2 =

Exploration Of Parabolas

Answered 4x X2 Consider The Parabola Y A Bartleby

1

Find The Area Of The Region Bounded By The Parabola Y 2 4x The X Axis And The Lines X 1 And Youtube

Solved Find The Centroid Of The Area Bounded By The Parabola 4x X 2 Y And Y 0 Course Hero

Volume Of Revolution Worksheet

Find The Area Lying Above The X Axis And Under The Parabola Y 4x X 2 Sarthaks Econnect Largest Online Education Community

Parabolas Ppt Download

Find The X Intercepts Of Thr Following Parabola Y 4x 2 8x 12 Brainly Com

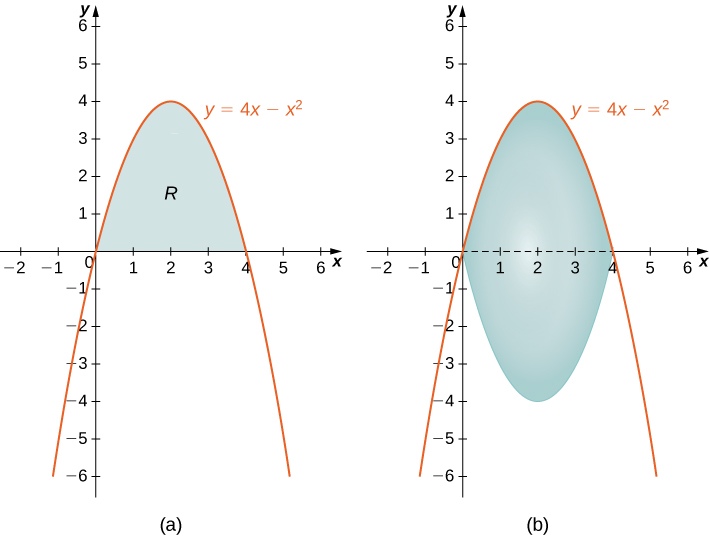
6 3 Volumes Of Revolution Cylindrical Shells Calculus Volume 1

Consider The Parabola Y 4x X2 A Find The Slope Chegg Com

The Area Bounded By The Curves Y 2 4x And X 2 4y Youtube

1

Sketch The Region R That Lies Below The Parabola Y 4x X 2 Above The X Axis And Above The Line Y 3x 6 Find The Area Of The Region R Study Com

Consider The Parabola Y 4x X2 A Find The Slope Chegg Com

View Question Given The System Of Equations Y X 2 4x X 4 The Number Of Points Of Intersection Is

Misc 15 Find Area X Y Y2 4x 4x2 4y2 9 Miscellaneous

1

Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube

Ex 8 2 7 Area Lying Between Y2 4x And Y 2x Is Ex 8 2

Exploration Of Parabolas

Hitunglah Luas Dataran Yang Dibatasi Oleh Parabola Y 4x X Dan Sumbu X Brainly Co Id

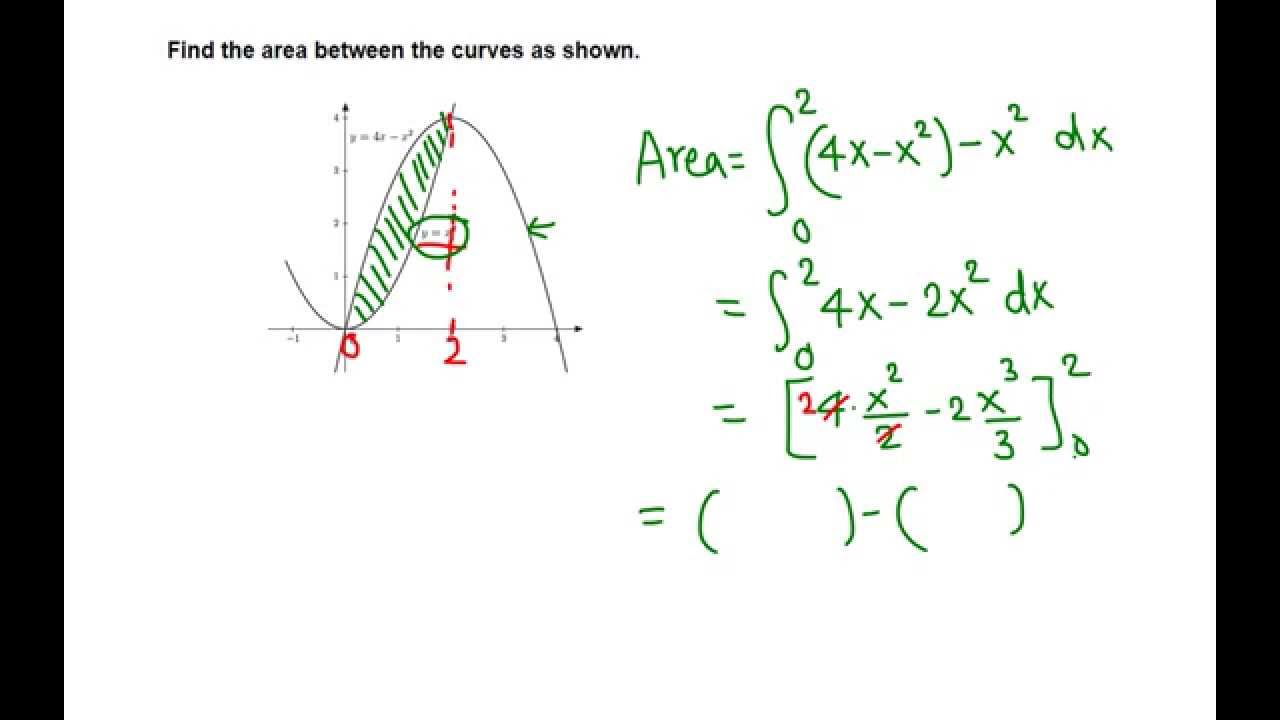
Area Between Y 4x X 2 And Y X 2 Youtube

The Area Bounded By The Parabola Y 4x X 2 And X Axis Is

What Is The Area Bounded By X Axis And The Curve Math Y 4x X 2 Math Quora

Find The Area Of The Region R See How To Solve It At Qanda

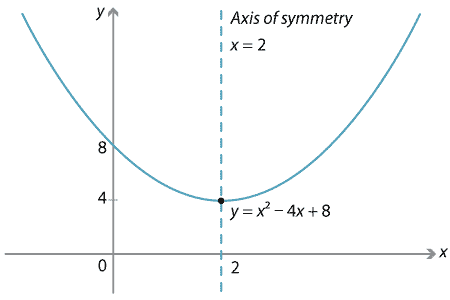
Content Transformations Of The Parabola

Solution Graph The Parabola Y X2 4x 6

Solution Find The Area In The First Quadrant Bounded By The Parabola Y 2 4x X 1 And X 3

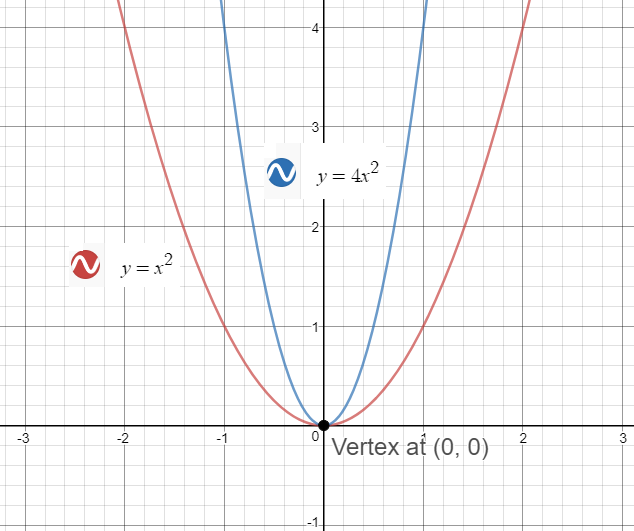
How To Graph A Parabola Y 4x 2 Socratic

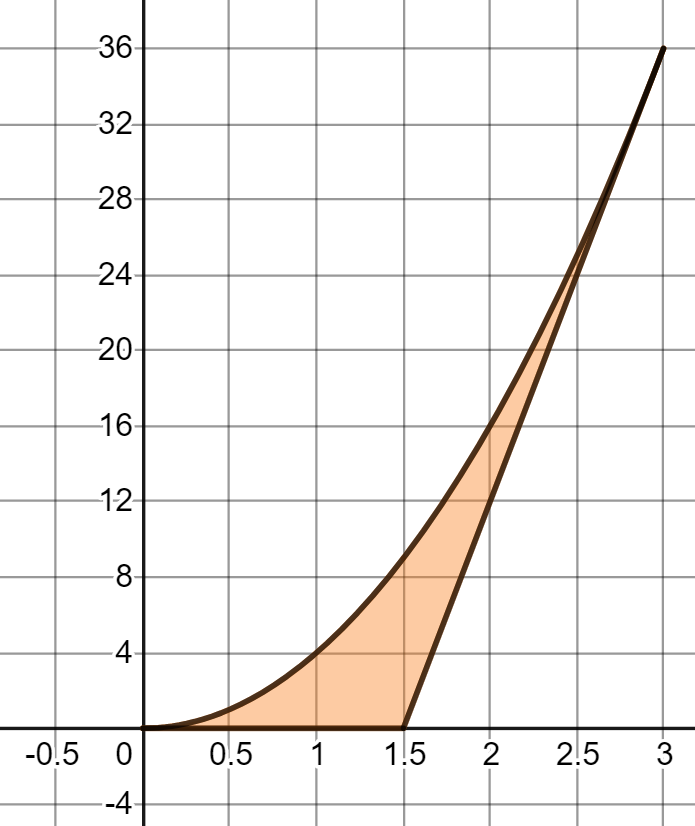
Find The Area Of The Region Bounded By The Parabola Y 4x 2 The Tangent Line To This Parabola At 3 36 And The X Axis Homework Help And Answers Slader

Find The Area Bounded By The Curve Y 4x X 2 The X Axis And The

Where Do Y X 2 4x 1 And Y 3 X Intersect Mathskey Com

Solved Consider The Parabola Y 4x X2 A Find The Slope M Of The Tangent Line To The Parabola At The Point 1 3 I Using This Denition The Course Hero

The Area Bounded By The X Axis And The Curve Y 4x X 2 3 Is

2 Find The Area Lying Above The X Axis And Under Gauthmath

Find The Area Of The Region Bounded By Y 2 4x X 1 X 4 And The

Find The Area Of The Region Bounded By The Curve Y2 2x And X2 Y2 4x Studyrankersonline

2

Example 14 Prove That Y2 4x X2 4y Divide Area Of Square

Aplikasi Integral Tertentu

Answered Parabola Y 4x X At The Point 1 3 Bartleby

The Point Of Intersection Of The Tangents To The Parabola Y 2 4x At The Points Where The Circle X 3 2 Y 2 9 Meets The Parabola Other Than The Origin Is

Search Q Area Between Two Curves Tbm Isch

Solved A Find The Slope Of The Tangent Line To

The Region Bounded By The Parabola Y 4x X 2 And Chegg Com

Consider The Parabola Y 4x X2 A Find The Slope Chegg Com

Find The Area Bounded By Y 2lt 4x X 2 Y 2geq2x A N Dxlt Y 2 In

Answered 2 A Region Bounded By The Parabola Y Bartleby

Example 7 Find Area Lying Above X Axis Included B W Circle

Consider The Parabola Y 4x X2 A Find The Slope Chegg Com

Determine The Area Of The Region Bounded By The Parabola Y 4x 2 The Tangent Line To This Parabola At 2 16 And The X Axis Study Com

Ex 8 1 11 Find Area Bounded By Y2 4x And Line X 3

Find The Area Of The Region Bounded By The Parabola Y 2 4x The X Axis And The Lines X 1 And X 4 Sarthaks Econnect Largest Online Education Community

Find The Area Lying Above The X Axis And Under The Parabola Y 4x X2 Maths Meritnation Com

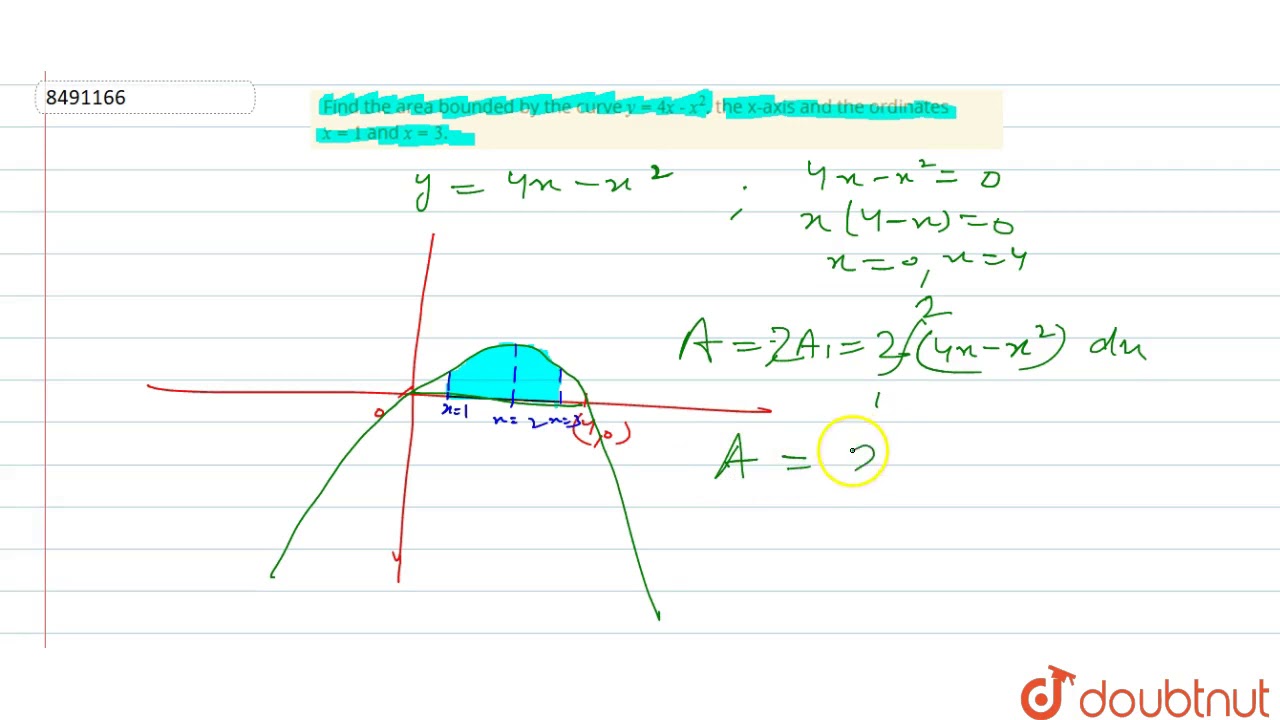
Find The Area Bounded By The Curve Y 4x X 2 The X Axis And The Ordinates X 1 And X 3 Youtube

Drill Find The Area Between The X Axis And The Graph Of The Function Over The Given Interval Y Sinx Over 0 P Y 4x X 3 Over 0 3 Ppt Download

Consider The Parabola Y 4x X2 A Find The Slope M Chegg Com

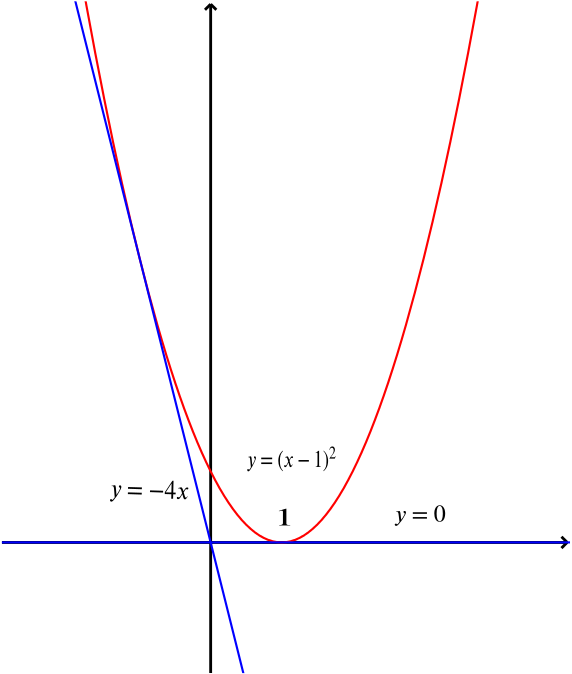
Solution When Does Y Kx Intersect The Parabola Y X 1 2 Quadratics Underground Mathematics

What Is The Area Bounded By X Axis And The Curve Math Y 4x X 2 Math Quora

The Area Bounded By The Curve Y 4x X2 And The X Axis Is Mathematics Shaalaa Com

The Graph Of Y 4x 4 Math Central

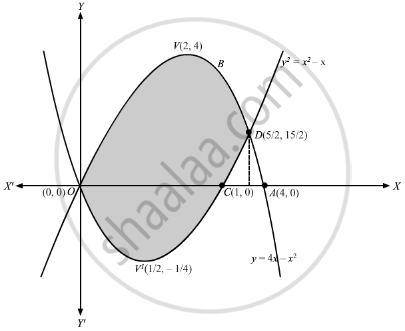
Find The Area Enclosed By The Parabolas Y 4x X2 And Y X2 X Mathematics Shaalaa Com

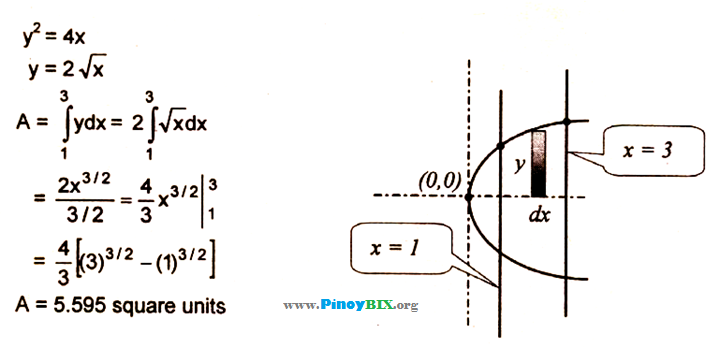
Solution Find The Area In The First Quadrant Bounded By The Parabola Y 2 4x

Question 3 Evaluate Yda Where R Is The Region Bounded By Y 4x And X Homeworklib

What Is The Volume Of The Region Bounded By Y 4x X 2 And Y X 2 If Rotated About The Line X 4 Quora

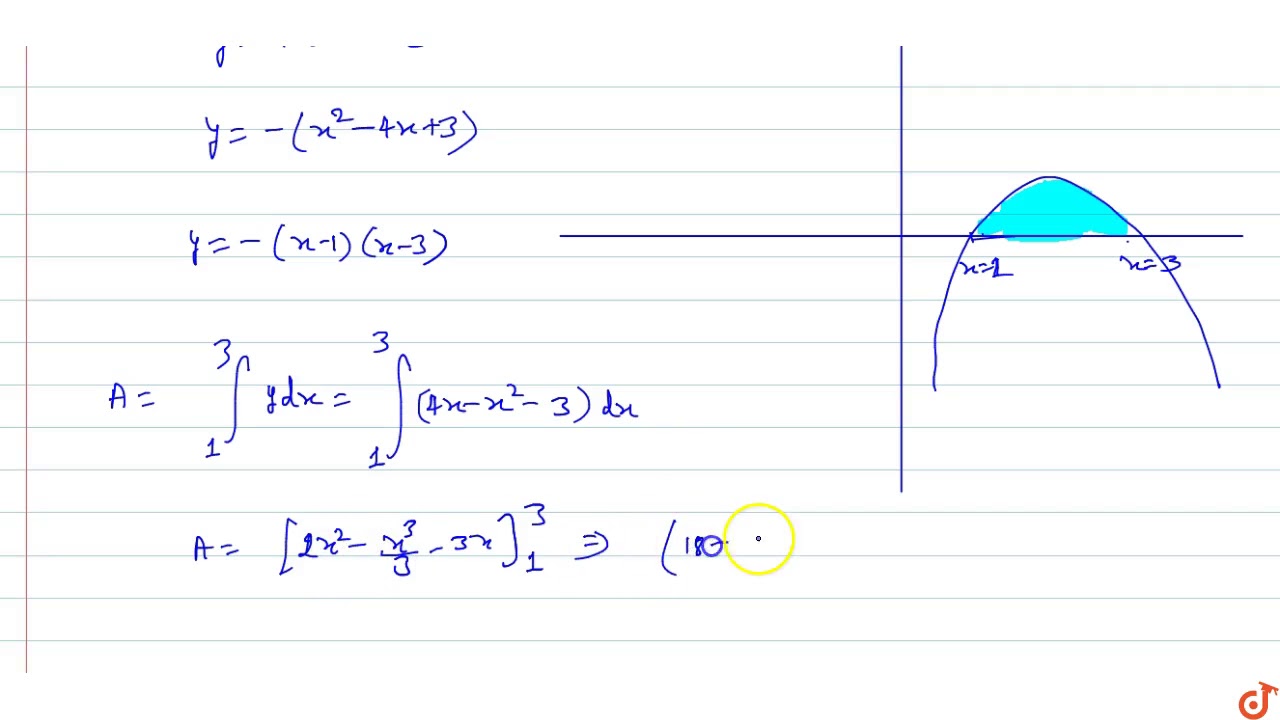
The Area Bounded By The X Axis And The Curve Y 4x X 2 3 Is Youtube

Parabolas

Find The Area Enclosed By The Parabolas Y 4x X2 And Y X2 X Maths Meritnation Com

Drill Find The Area Between The X Axis And The Graph Of The Function Over The Given Interval Y Sinx Over 0 P Y 4x X 3 Over 0 3 Ppt Download

What Is The Area Bounded By The Curve Y 4x X And The Lines X 0 And Y 4 Quora

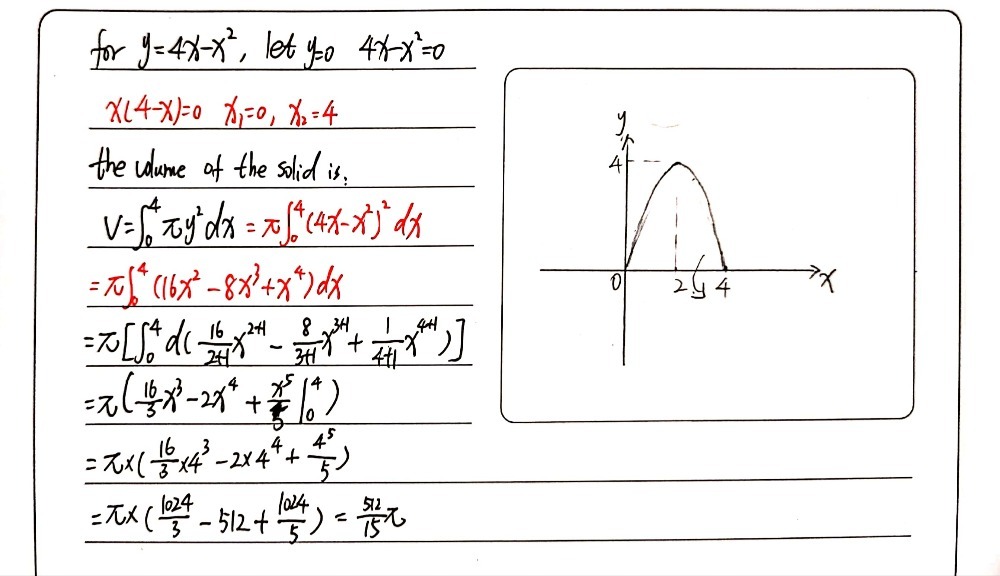
Q1 The Region Bounded By The Parabola Y 4x X2 And Gauthmath

The Are Bounded By The Curve Y 4x X 2 And The X Axis Is

Find The Area Of The Segment Cut Off From The Parabola Y 2 2x By The Line Y 4x 1 Sarthaks Econnect Largest Online Education Community

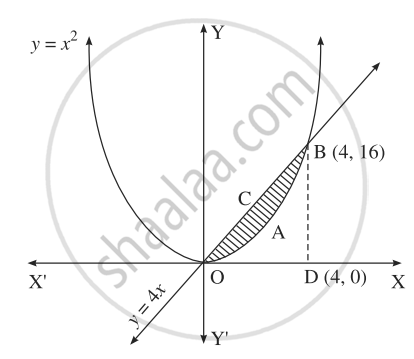
Find The Area Of The Region Included Between Y X2 And The Line Y 4x Mathematics And Statistics Shaalaa Com

How Do You Find The Area Between The Curves Y 4x X 2 And Y X Socratic

The Area Bounded By The Parabola Y 4x 2 Y X 2 9 And The Li

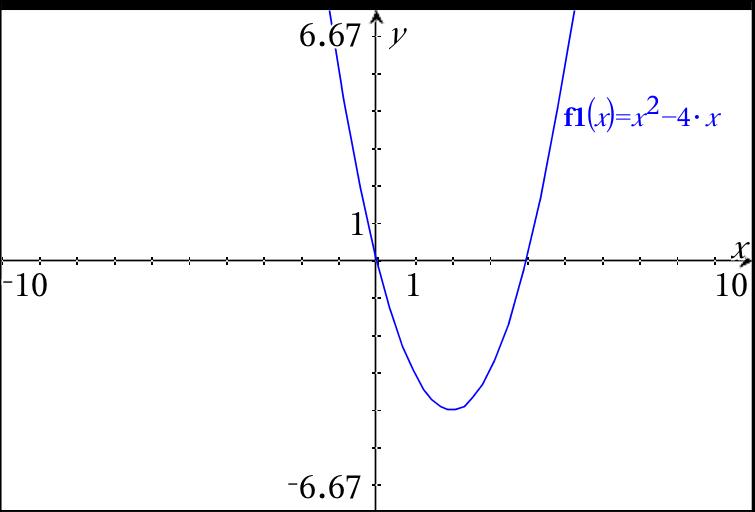
What Is The Graph Of F X X 2 4x Socratic

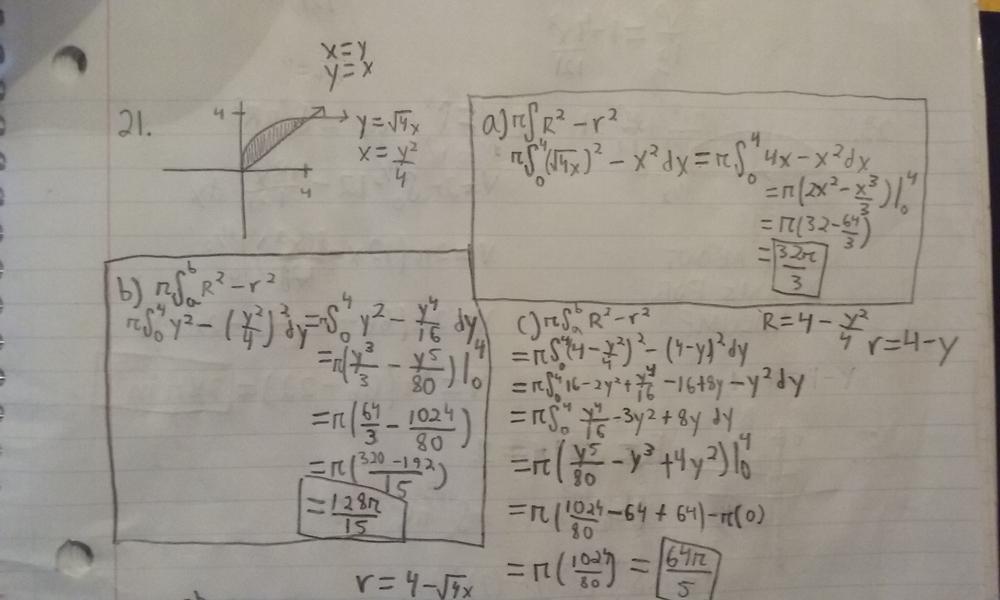
Find The Volume Of The Solid Generated By Revolving The Region Enclosed By The Parabola Y 4x And The Line Y X About A The X Axis B The Y Axis C

2 Find The Area Lying Above The X Axis And Under Gauthmath

Incoming Term: parabola y=4x-x^2, consider the parabola y=4x-x^2, parabola y=x^2+4x-5, parabola y=x^2-4x-12, the parabola y^2=4x and x^2=4y, the region bounded by the parabola y=4x-x^2, how does the parabola open y=4x-x^2-1, vertex of parabola y=x^2+4x+3, graph the parabola y=x^2-4x+5, graph the parabola y=x^2-4x+3,