球面上の多角形の面積と内角の和には美しい関係がある, というのが冒頭の定理です。三角形の場合が本質的です(証明は球面上の三角形の面積と内角の和を参照して下さい)。 三角形の場合を認めれば一般の n n n 角形については簡単に証明できます!座標上の多角形の面積 #1 使えそうで使えない、だけどチョットだけ使えそうなオリジナル公式。 早稲田大学院生だったO君と開発したので、OK 定理とでも名付けましょうか。 座標上にある三角形P 1 P 2 P 3 の面積は、次のように求められる。 これは 平面図形の面積の求め方の公式 多角形の面積の求め方 長方形=縦×横 正方形=1辺×1 中学受験に塾なしで挑戦するブログ―やってみてる編 塾に通わずに中学受験はできるのか?

如何求正多边形的面积 7 步骤
多角形 面積 公式 小学生
多角形 面積 公式 小学生-概要 多角形の面積を計算する。 多角形の面積を求める公式が存在し、\(N\)個の点\(\mathbf{p_i} = (x_i, y_i)\)から成る多角形の面積\(S\)は以下の式で計算できる。ひし形の面積の公式 ひし形の面積は 2 2 つの対角線の長さをかけて2で割ったもの、つまり 『対角線×対角線÷2 ÷ 2 』 で求めることができます。 平行四辺形の一種でもあるので、底辺と高さが分かっていれば『底辺×高さ』でも求められます。 たとえば



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典
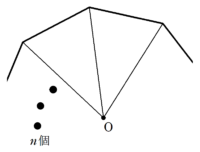
円に内接する四角形 $\mathrm {ABCD}$ において, $a = \mathrm {AB},$ $b = \mathrm {BC},$ $c = \mathrm {CD},$ $d = \mathrm {DA},$ $s = \dfrac {abcd} {2}$ とおく このとき, 四角形の面積5 定理の公式と上記の格子多角形の面積を求める計算例 S = m + n / 2 S:格子多角形の面積 m:完全な枠(格子1マス)の数(下図のピンクの枠) n:不完全な枠(1本の辺と格子枠に囲まれている枠)の数(下図のグリーンの枠)に対する面積公式 一般には Robbins5 の公式 (1994) とよばれるが,ここでは,Pech4 による定式化を示し,これをもと に次節で,面積・半径の統合公式の導出を試みる.各変数は,図2 に示された座標および辺対角線の長さ
Ⅰ 面積の公式 1辺 \(~a~\) の正四角形(正方形)の面積の公式は誰でも知っていますが、正三角形の面積の公式は答えられない人が多いのではないでしょうか。 しかし、正三角形は定期テストや入試でよく登場する図形であり、面積が必要となる場面も少なくありません。 「39回の場合は、面積公式、これは、3次元空間上の任意の平面にある多角形の各頂点の位置ベクトルを、r j としたとき、 (添え字 jは、多角形を上から見て、反時計回りに1~nまで振ったものとしよう。n>=3)という $u_{2}$ に関する 7 次方程式を得る.ただし,crossing parity $\epsilon$ の値は, $0$ ( 五角形 ) $1$ ( 凸六角形 ) $1$ ( 非凸
三角形の面積公式の証明 冒頭に述べた球面三角形の面積公式 s = r 2 (a b c − π) s=r^2(abc\pi) s = r 2 (a b c − π) を証明します。 まず二つの大円のなす角が a a a である状況を考えます。二つの大円によって球面は4つに分割されます。 Ⅰ 面積の公式 以前の記事で、正三角形から正六角形までの面積の求め方を紹介しました。(「正多角形の面積の公式」を参照) 今回は、正 \(~n~\) 角形の面積、つまり一般化してみたいと22 円内接五角形に対する統合公式 既知の方法 6 5 2 により,半径公式 (2,922項) は既に求められているものとする.



改革春风吹满地 多边形面积的求法 用到矩阵 Dsh0106的专栏 Csdn博客




多邊形面積 1 Youtube
出典 フリー百科事典『ウィキペディア(Wikipedia)』 ( 59 UTC 版) 面積公式 多角形の面積は、頂点の位置ベクトルから外積を用いて計算することができる。 多角形の頂点を反時計回りに並べて、それらの位置ベクトルを →, , → とすると、その面積は = → →面積公式 多角形の面積は、頂点の位置ベクトルから外積を用いて計算することができる。 多角形の頂点を反時計回りに並べて、それらの位置ベクトルを →, , → とすると、その面積は 面積の求め方の基本(たて×よこ) 小学生の算数で習う多角形の 面積の公式で一番の基本 は タテ×ヨコ です。



利用行列式計算多邊形面積 線代啟示錄




六角形面積公式正六邊形 Utvos
1.大まかに言って, 多角形の面積 ≒ 多角形に含まれる格子点の数 という関係があることは確かである 何か見付かるかもしれないので, いくつか具体的な多角形をとって, 2つの量を比べてみたい 2.多角形に含まれる格子点の数には次の2種類がある: 3.多角形の面積 S は n と N の中間多角形の座標入力で簡易に面積計算出来るので役に立つ。 アンケートにご協力頂き有り難うございました。 送信を完了しました。 座標点で囲まれる多角形の面積 のアンケート記入欄 性別 男 女 年齢 歳未満 歳代 30歳代 40歳代 50歳代 60歳以上三角形の面積の公式 三角形の面積 = 底辺 × 高さ ÷ 2




正三角形面積公式證明從三角形的面積談起 Mrsysy



三角形面积计算公式 三角形面积公式 越多越好 100查分网
正多角形の面積 sqrt (xx) のように指定してください。 正多角形の1番長い対角線の長さを表示してほしい。 1辺を1としたときと仮定した時でいいので。 非常に役に立った。 立式できても計算に時間が取られていたが、こちらのサイトで瞬時に答えが出た13 多角形の面積の公式および向き (頂点列の回転方向) の判定方法 面積 S≡∫dS は断面0次モーメントなので, 断面N次モーメントの公式 で N=0 と置けばよい. ここで P i ×P i1 は 2次元の外積 である. S の符号は C の回転方向によって変わる. つまり S多角形の辺は,内部を左に見るように方向付けられていると仮定. すなわち,多角形の辺は反時計回りの順を仮定. 0 1 1 1 1 1 0, ( ), 2 1 ( ) n n i i n i i y y y y area P x y y ただし, 上記の符号付面積> 0 多角形は反時計回り < 0 多角形は時計回り




正投影公式祖暅原理與正投影面積公式 Mrsysy




计算六角形的面积 建议 August 21
数学・算数 多角形の面積比について 三角形の面積比は相似比の二乗となると思いますが、これは八角形など、どんな多角形にも応用できるのでしょうか? 質問No図21 格子多角形の例 22 ピックの公式の初等的証明 以下しばらくの間は、単に格子多角形というと、連結で境界がただ一つの 単純閉曲線であるものを考えることにする。 定理21 (ピックの公式) 格子多角形P の面積Area(P) は、P の内部この講習では、平面上の多角形であって、x 座標、y 座標がともに整数である多角形(格子多角 形) の面積を中心に解説します。格子多角形の面積公式としては、ピックの定理が有名ですが、加 えて、類似の定理である、森原の定理や額賀の定理も紹介します。



周长 面积 体积 玄数



三角形面积计算公式 三角形面积公式 越多越好 100查分网
三角形の面積を求める公式は 三角形の面積 底辺 高さ 三 角 形 の 面 積 = 底 辺 × 高 さ ÷ 2 なので、 三角形の面積 三 角 形 の 面 積 = 6 × 4 ÷ 2 = 24 ÷ 2 = 12 ( c m 2) になります。 次は小数点を含む三角形の面積を計算します。古典幾何における内接多角形の面積公式 早稲田大学大学院基幹理工学研究科数学応用数理学専攻 梅澤瑠奈(Runa UMEZAWA) 1 はじめに ユークリッド幾何では三角形のときHeron の公式, 内接四角形のときBrahmagupta の公式など、面積をその辺正しい公式を覚える 通常の多角形の面積 (は (a x p)/2 で求められます。 この時、 a とは辺心距離の長さを、 p は多角形の外周を意味しています。 4



数学7年级3角形面积 西瓜视频搜索




基測數學 094v2 單選25 六邊形面積 Youtube
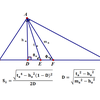
正多角形の面積を求めます。 高校数学の問題集に載ってるレベルの問題です。正 角形の1辺の長さを 、重心(正 角形の外心と一致する) o と頂点の距離を (これは外接円の半径でもある)とします: 図中の点 a, b は正 角形の隣り合う頂点、点 m は辺 ab の中点です。公式の導出方法 正多角形の面積導出には、sinで表す三角形の面積公式 1 2 sin θ a b を使用します




如何计算六角形的面积 提示 August 21



四边形的面积公式 知乎




如何求正多边形的面积 7 步骤




常用圖形求面積計算公式 人人焦點



五年级数学知识点总结 04多边形面积 知乎




计算六角形的面积 建议 August 21




等边直三角形面积公式 西瓜视频



锐角三角形的计算公式 3角形面积计算公式 尚书坊




正三角形面積公式證明從三角形的面積談起 Mrsysy




小三 周長與面積 求正多邊形周長 重點講解 Youtube




利用向量積 叉積 計算三角形的面積和多邊形的面積 碼上快樂



50 多角形面積公式 ニーアオートマタ壁紙




計算任意多邊形的面積 已知各頂點的坐標 碼上快樂




如何求正多边形的面积 7 步骤



正多角形の面積の公式 一般化 Fukusukeの数学めも




六角形面積公式正六邊形 Utvos




多边形面积 Segmentfault 思否



八角形面積計算八角形面積公式 百度知道狀態 Ekcup




等边三角形面积公式 Csdn



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典




解析一道經典小學數學多邊形面積計算題 組合圖形面積計算 好題 雪花新闻




国际数学竞赛 任意多边形面积计算公式 知乎




数学趣谈 球面积公式的不同导出方法 参考网




用三角形面積公式 揭開了鮮為人知的小秘密 顛覆了學數學的認識 每日頭條




利用行列式計算多邊形面積 線代啟示錄



六角形面积怎么计算 西瓜视频搜索




如何求正多边形的面积 7 步骤



四边形的面积公式 知乎




三角形的几个面积公式都是什么时候发现的 网易订阅
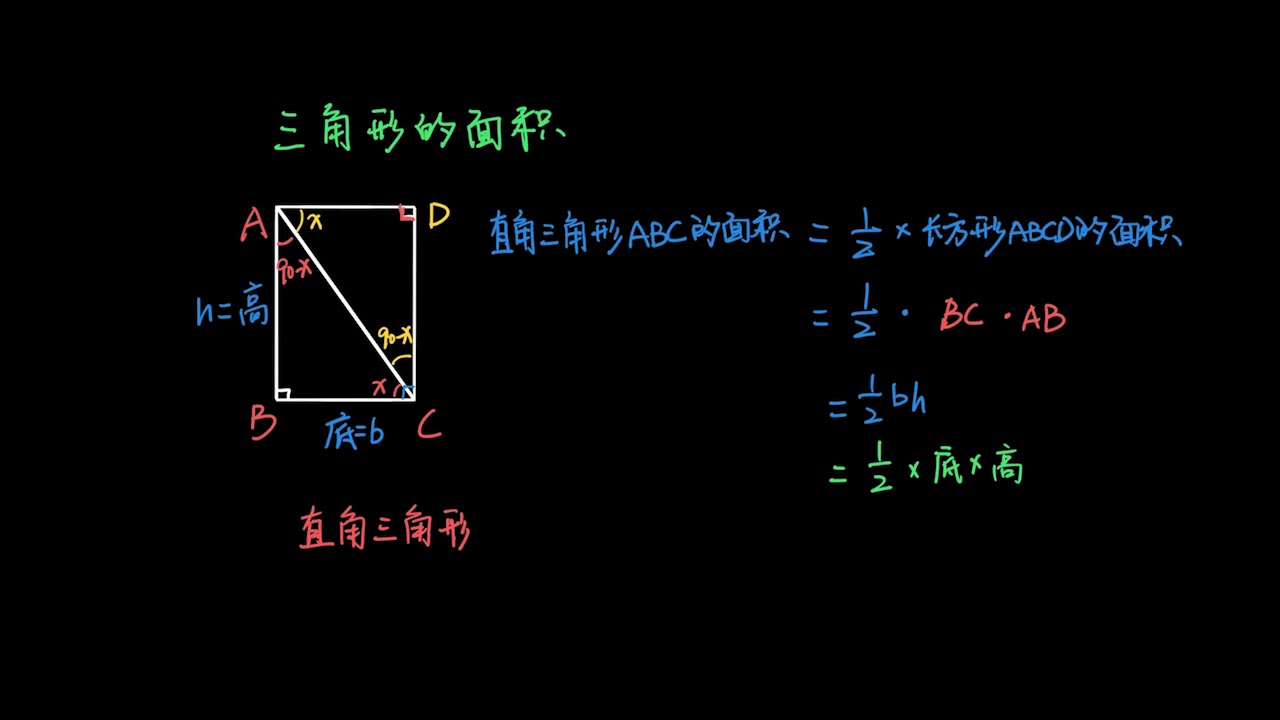



五年级数学41 多边形的面积 三角形面积公式证明 Youtube




三角形正多边形面积公式 三角形png图片素材免费下载 图片编号 Png素材网




高能預警 多邊形面積如何計算 小心被虐哭 一 每日頭條



1



三角形面积公式小学 搜狗图片搜索




六边形面积怎么算 百度经验



高中数学 纯干货 三角形的30个面积公式总结 高中生快来收 初中




计算六角形的面积 建议 August 21
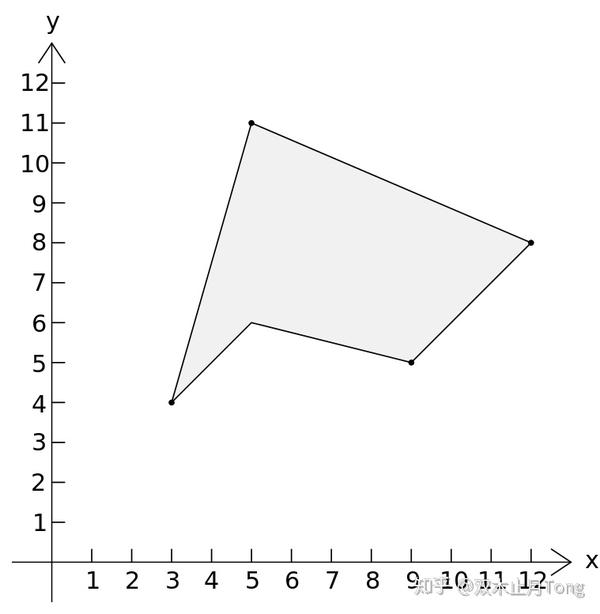



国际数学竞赛 任意多边形面积计算公式 知乎




解析一道經典小學數學多邊形面積計算題 組合圖形面積計算 好題 雪花新闻
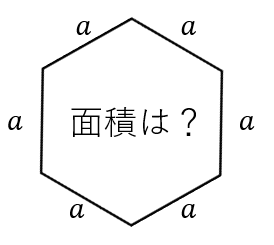



正六角形の面積 計算ツール 公式の導出 具体例で学ぶ数学



1




初中 簡單多邊形面積公式 Youtube




預測與驗證平面凸多邊形面積公式 I




海龍公式 維基百科 自由的百科全書




八边形 维基百科 自由的百科全书



1




五邊形面積計算利用行列式計算多邊形面積 Txfs Co




50 多角形面積公式 ニーアオートマタ壁紙




八角形面積計算八角形面積公式 百度知道狀態 Ekcup



五邊形面積公式超實用的高中數學公式 扇形的表面積計算 Kmgrkz




三角函數六角形正多角形の面積 Pbhcl




如何求正多边形的面积 7 步骤



Http Euler Tn Edu Tw Area Pdf




梯形面積對角線三角形 平行四邊形 梯形 多邊形面積公式怎麼記 親子天下 Qavhp




正多边形面积 内角和 外接圆 内切圆在线计算器 三贝计算网 23bei Com



等边三角形面积公式计算器 等边三角形面积计算 七月seo



高中数学 纯干货 三角形的30个面积公式总结 高中生快来收 初中
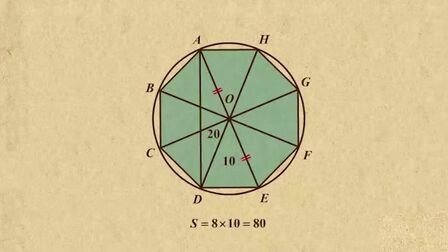



正八边形面积公式 搜狗搜索
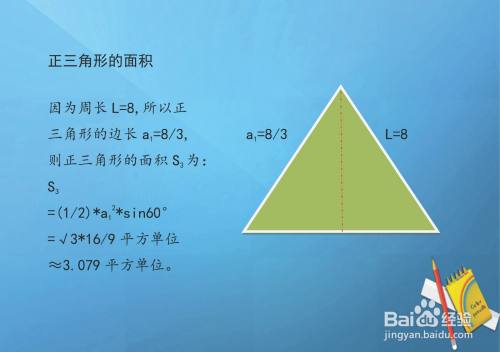



已知周长l 8 求正三角形等多边形和圆的面积 百度经验



等腰三角形面积公式 等腰三角形面积公式 尚书坊




等腰三角形周長公式等腰三角形公式 等腰三角形周長公式 等腰三解形面積公式 Vnfp



利用行列式計算多邊形面積 線代啟示錄




一般 正三角形的高與面積 Youtube



利用行列式計算多邊形面積 線代啟示錄




数学趣谈 球面积公式的不同导出方法 参考网




五邊形面積計算利用行列式計算多邊形面積 Txfs Co
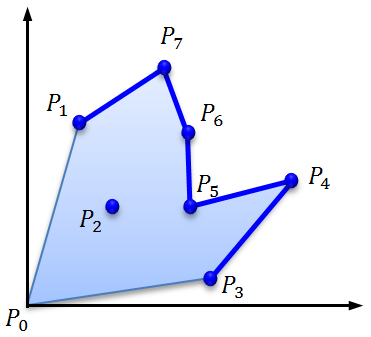



N点からなる多角形の面積を求める イメージングソリューション



八角形面積計算八角形面積公式 百度知道狀態 Ekcup




計算任意多邊形的面積 已知各頂點的坐標 碼上快樂




面積計算公式gmath Pripdw




平面上任意多邊形求面積的方法 Youtube



锐角三角形的计算公式 3角形面积计算公式 尚书坊



三角形面积公式小学 搜狗图片搜索



1



六邊形面積公式六邊形 Kdnbe



六角形面积怎么计算 西瓜视频搜索




高校数学 正多角形の面積の求め方 練習編 映像授業のtry It トライイット




直角锥体积 表面积 侧面积 计重 报价计算公式与在线计算器 三贝计算网 23bei Com




如何求正多边形的面积 7 步骤




多边形的面积 天明天明 博客园




Pk Ckcos6 正多邊形面積公式




4种方法来求六边形面积




五年級數學月考必備 多邊形的面積計算單元重點 老師嘔心總結 每日頭條




计算六角形的面积 建议 August 21



数学7年级3角形面积 西瓜视频搜索



課堂實錄 圓的面積 六上 雪花新闻



等边三角形面积公式表 等边三角形面积计算 七月seo



周长 面积 体积 玄数
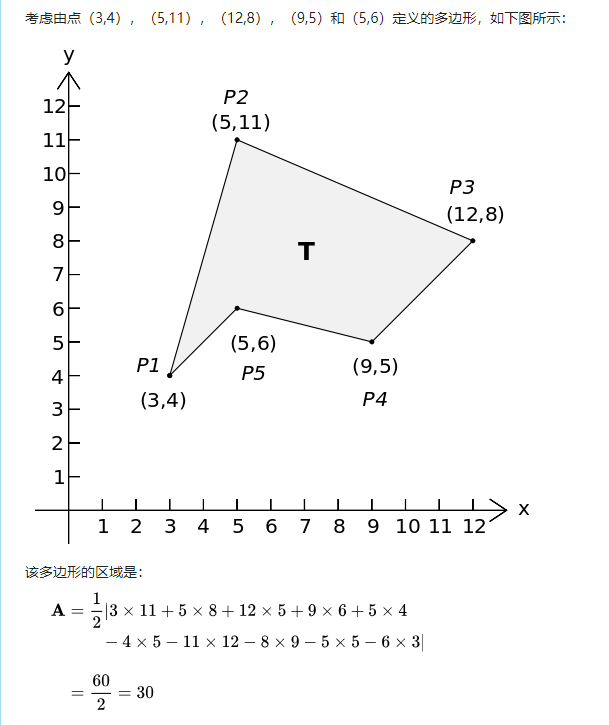



C 多边形面积计算公式 Khandasas 博客园




八角形计算公式 八角形有哪些计算公式 三人行教育网 Www 3rxing Org
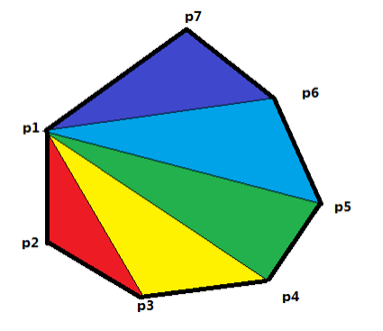



多边形的面积 天明天明 博客园




如何计算多边形面积 15 步骤



0 件のコメント:
コメントを投稿