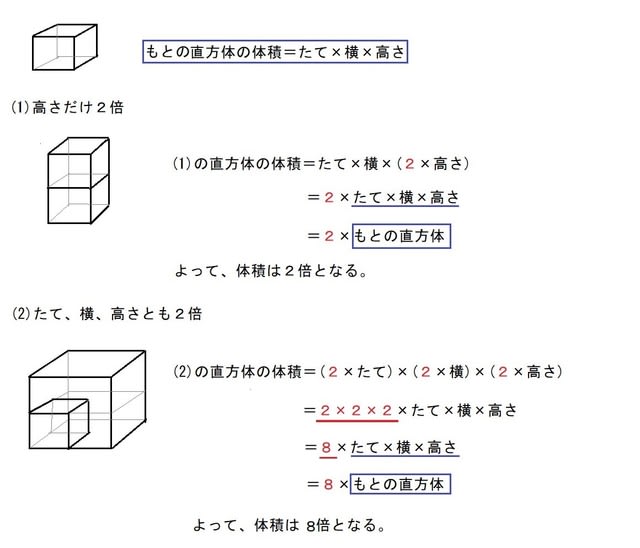
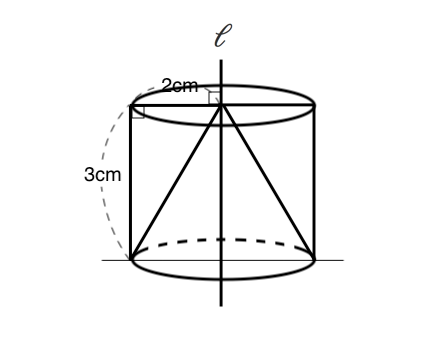
活用問題 小学校 算数科 第5・6学年 トップ>小学校算数科 研究概要版 研究本文 補助資料 活用問題を利用するに当たって 活用問題一覧表 問題番号 単元 活用問題 正答例と解説 1 5年「整数と小数」 2 5年「直方体や立方体の体積」 3このページは、 小学5年生が立体の体積について学習するための「直方体や立方体の体積の問題集」が無料でダウンロードできる ページです。 この問題のポイント ・ 直方体の体積は、「たて×横×高さ」で求めることができます。 ・ 立方体はすべての辺北海道大学 理系 a,bを正の実数とする。 xyz空間内の2点 A(a,0,0),B(0,b,1)を通る直線を lとし、直線lを z 軸のまわりに一回転して得られる曲面をMとする。 1P(x,y,z)を曲面M上の点とする。このとき x,y,zが満たす関係 式を求めよ。 2曲面Mと2つの平面 z = 0と z = 1で囲まれた立体の体積を求

立方体 直方体の体積の求め方 公式 小学生 中学生の勉強
立体の体積 問題5年
立体の体積 問題5年-小学5年生の算数直方体と立方体を組み合わせた立体の体積を求める問題プリントを無料ダウンロード・印刷 (プリント5枚) 小学5年生の算数 多角形の角 三角形の角 問題プリント問題一括 (2,135Kb) 解答一括 (2,0Kb) 小数の表し方 整数と小数のしくみ 2 直方体や立方体の体積 体積の意味 問題一括 (6,079Kb) 解答一括 (6,325Kb) 体積の意味 直方体、立方体の体積(1) 直方体、立方体の体積(2) 直方体の横の長さと体積の関係 いろいろな体積の




三角柱の体積の求め方 小学生向けに問題使って解説するぞ 中学数学 理科の学習まとめサイト
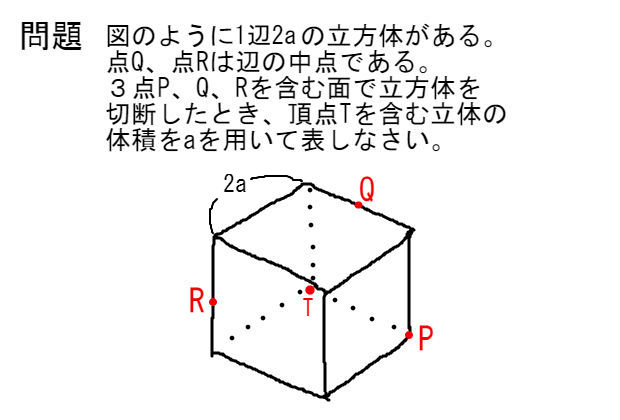
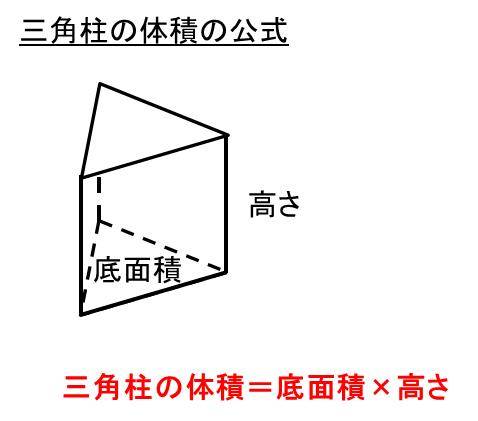
== 立体の体積(入試問題) == 要点四角柱,三角柱,円柱の体積 四角柱,三角柱,円柱の体積 V は,底面積 S と高さ h を使って表すことができます.動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru今回は立体S、つまり辺NGを含む立体の体積を求める問題です。 立体Sの形を考えます。 まずは、今見つけた2つの交点を結びます。 これで2つの切り口も直線AIによって、それぞれ2つの部分に分けら
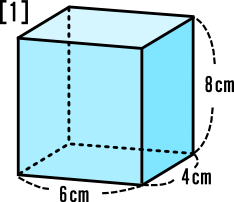
<体積と容積の問題>図1 のような直方体の容器に水を入れました。図2のグラフは, この ときの水 を入れ始めてからの時間 と,容器にたまった水の深さとの関係 を表 した ものです。 これについて,次 の間いに答えなさい。 問題1)下の図1の立体の体積を求めよ。 問題2)下の図2の長方形ABCDを、線分ABを回転の軸として1回転させてできる立体の体積は63 \(\pi\) ㎤だった。線分ABの長さを求めよ。 問1)30㎤ 問2)7cm立体図形の総合問題(桜蔭中学 13年) 円すいを切った体積(大妻中学 13年) 長さ比と体積比は?(開成中学 過年度) 残った立体の体積は?(早稲田中学 14年) 表面積と体積は?(明星中学 10年) この立体図形の体積は?
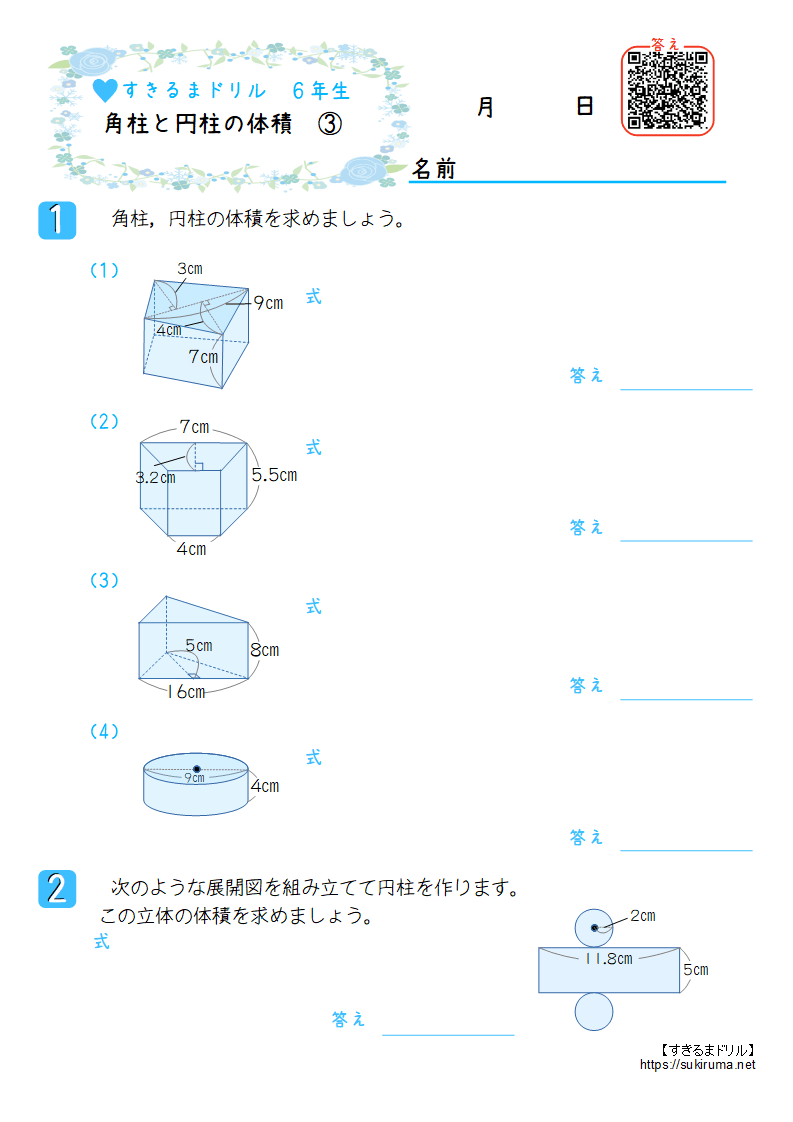
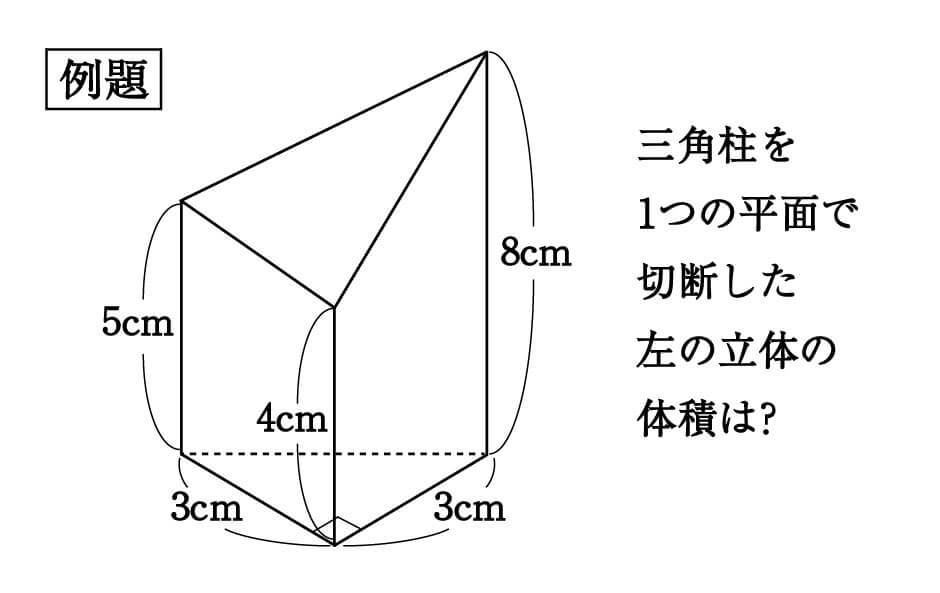
問題)体積は? 立体図形を斜めに切断した時の体積は底面積×高さの平均 答え)80cm 3 以上、基本問題でした。5年生の段階では、基本問題を「完璧」に 解ける事が大事です。 まとめ 立体図形を斜めに切断した時の体積は底面積×高さの平均2 次の展開図を組み立てて、できあがる立体の体積を求めましょう。 ① 式 長方形の横の長さは、円周と同じ長さなの 体積8 17年12月17日 19年2月9日 不等式で表された立体の体積を求める問題です。 1. B (和歌山県立医大) とする.不等式 を満たす領域について (1) この領域と平面 との共通部分の面積 を求めよ. (2) この領域の体積を求めよ.



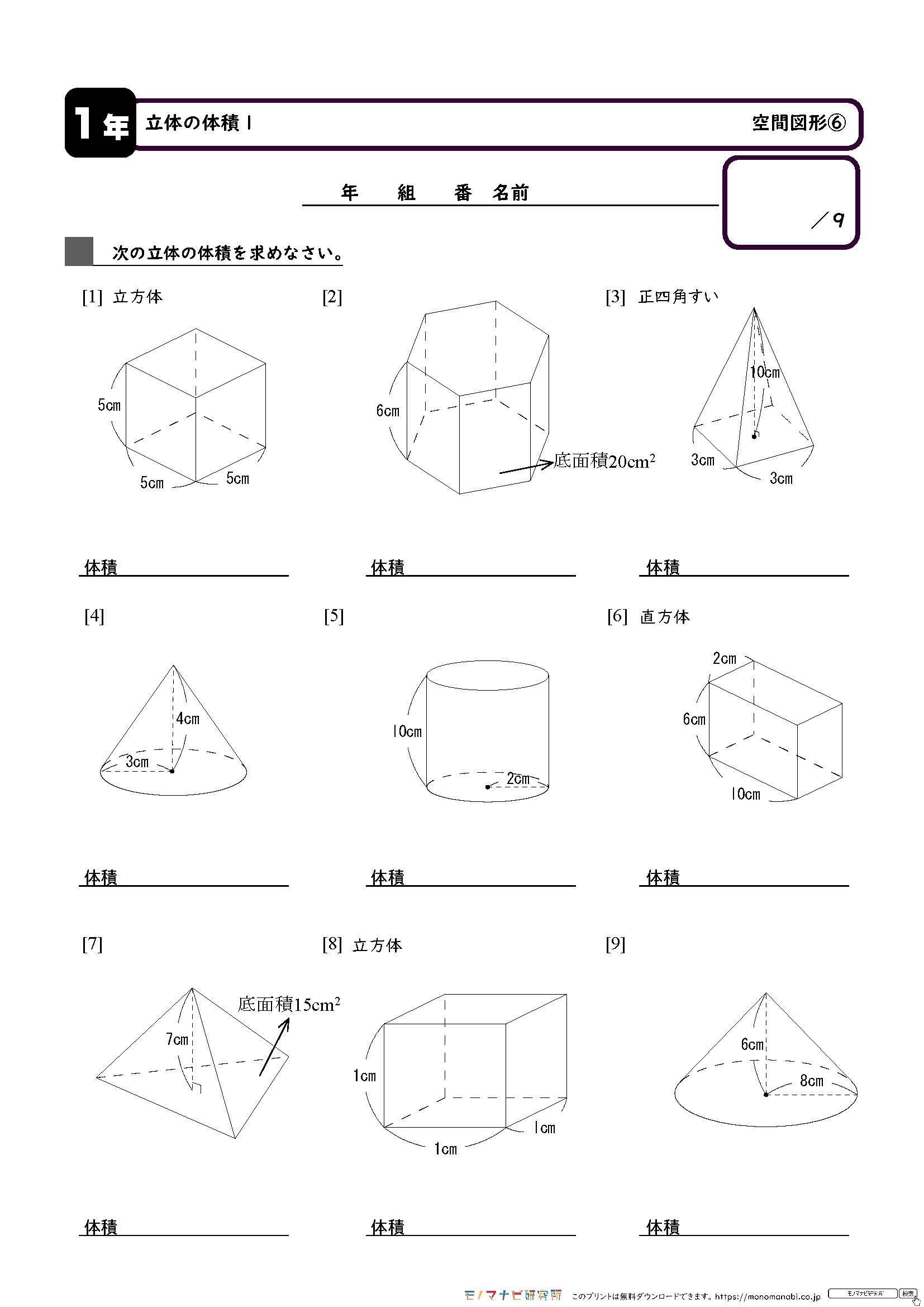
無料 中1数学 基本問題 問題プリント 空間図形6 立体の体積 143




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット
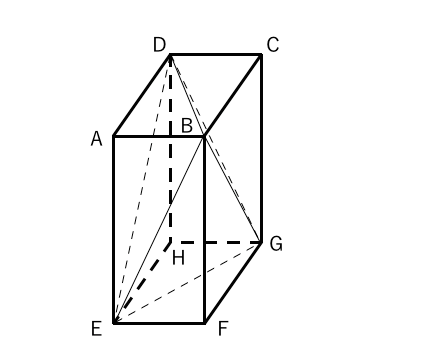
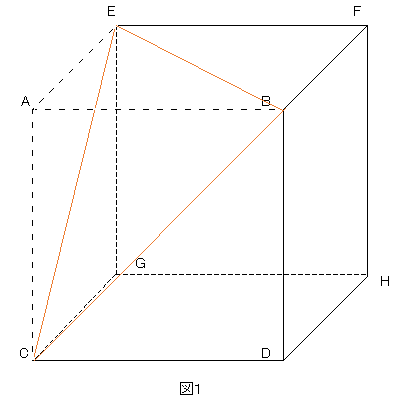
次のそれぞれの立体の体積を求めよ。 10cm cm 3cm ① 3cm 12cm ② 3cm 25cm 4cm 12cm ③ 10cm 3cm ④ 12cm 5cm 底面は正方形 ⑤ 図は 1 辺 12cm の立方体である。 この立方体の頂点 A, C, F を通る平面で切断する。 (1) 切断してできた2つの立体のうち 頂点Bを含むほうの立体は何という形か。 (2) (1)の立体の体積を求めよ。 A B C D E F G H図形問題 立体と体積・小学生算数問題テーマ 体積をしらべよう1 (一般的な直方体) 体積をしらべよう2 (変則的な直方体) 図形問題 立体と体積・小学生算数ドリルのページへようこそ 上記のボタンから図形問題 立体と体積・小学生算数ドリル(pdfプリント)がダウンロードできます。10×10×314+××314+ ×314×12+40×314×10=cm2。 解答:(1)体積875cm3 表面積600cm2 (2)体積5495cm3 表面積1927cm2 (3)体積cm3 表面積cm2 5. 右の(1)は直方体に円柱をさしこんだ もので、(2)は立方体に1辺8cmの 正方形を底面とする直方体で反対 側の面までくりぬいたものです。



毎日問題を解こう 18 苦手な数学を簡単に




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強
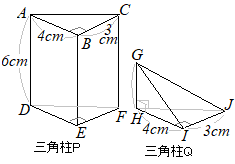
中学1年生 数学 空間図形立体の体積と表面積 練習プリント 無料ダウンロード・印刷 中1数学 空間図形立体の体積と表面積の問題を練習できる教材プリント。無料ダウンロード・印刷できます。図のように 1 辺6cm の立方体がある。 (1) 4点 A, C, F, H を頂点とする立体の名称を答えよ。 (2) (1)の立体の体積を求めよ。 図は底面が∠CAB=∠FDE=90°の直角三角形の 三角柱である。 この立体を面 PQR で切断する。 AB=6 ㎝、AC=4 ㎝、AD=12 ㎝、BQ=6 ㎝、 AP=9 ㎝、CR=8 ㎝のとき、切断してできる小さ いほう (下のほう)の立体の体積を求めよ。 右の図のように 1 辺 6cm の立方体立方体と直方体って何が違う? 立方体の体積問題を解説! まとめ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる! こちらの関連記事はいかがでしょうか?



この立体の体積は 2015年 成城学園中学 これが中学入試に出た図形問題




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強
熊本大学数理科学総合教育センター 3(9)(立体の体積2) 球x 2y z 25 4a2 と円柱x y2 5 a の共通部分E の体積を求めよ. 解 x 2y z2 5 4a 2よりjzj 5 p 4a x2 y2 だから, E = n (x;y;z) x 2y2 5 a ;問題6 (回転体の体積) 右の図のように,半径3cm,中心角90°のおうぎ形 がある。このとき と弦 で囲まれた部分を直線 を軸として1回転させてできる立体の体積を求めよ。Jzj 5 p 4a2 x2 y o と表される.ゆえに, Vol(E) = ZZZ E dxdydz = ZZ fx2y25a 2g dxdy




立体の体積問題 慶応義塾普通部 12年 恋する中学受験 大学受験を見据えた中学受験



Mathematics 錐体の一部の体積 働きアリ
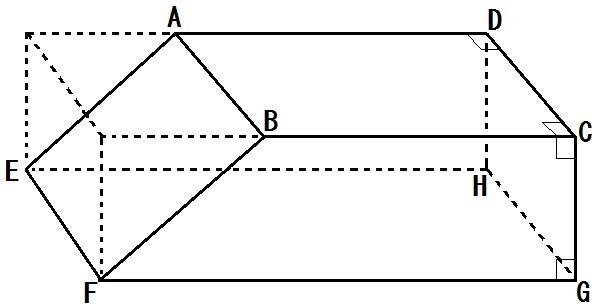
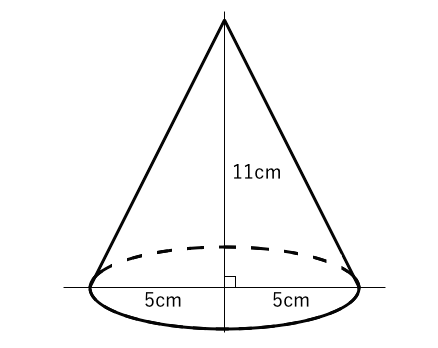
残った立体の体積を求めよ。 学基本学習の基本 33 角錐の体積と表面積 (錐体の体積)= 1 3 ×(底面積)×(高さ),(錐体の表面積)=(側面積)+(底面積) 問題 右の図の正四角錐の体積と表面積を求めよ。 解 体積 1 3 ×102× 12=400 (cm3)<問題に挑戦★> 右の図のような,半径が1 cmで,中心と直線l との距離が5 cmである円を,直線l のまわりに1回転させてできる ドーナツ形の体積を求めましょう。立体図形の総合問題(桜蔭中学 13年) 円すいを切った体積(大妻中学 13年) 長さ比と体積比は?(開成中学 過年度) 表面積と体積は?(明星中学 10年) この立体図形の体積は?(世田谷学園中学 14年) 特殊な立体図形の体積は?




三角柱の体積の求め方 小学生向けに問題使って解説するぞ 中学数学 理科の学習まとめサイト




立体の体積 無料で使える中学学習プリント
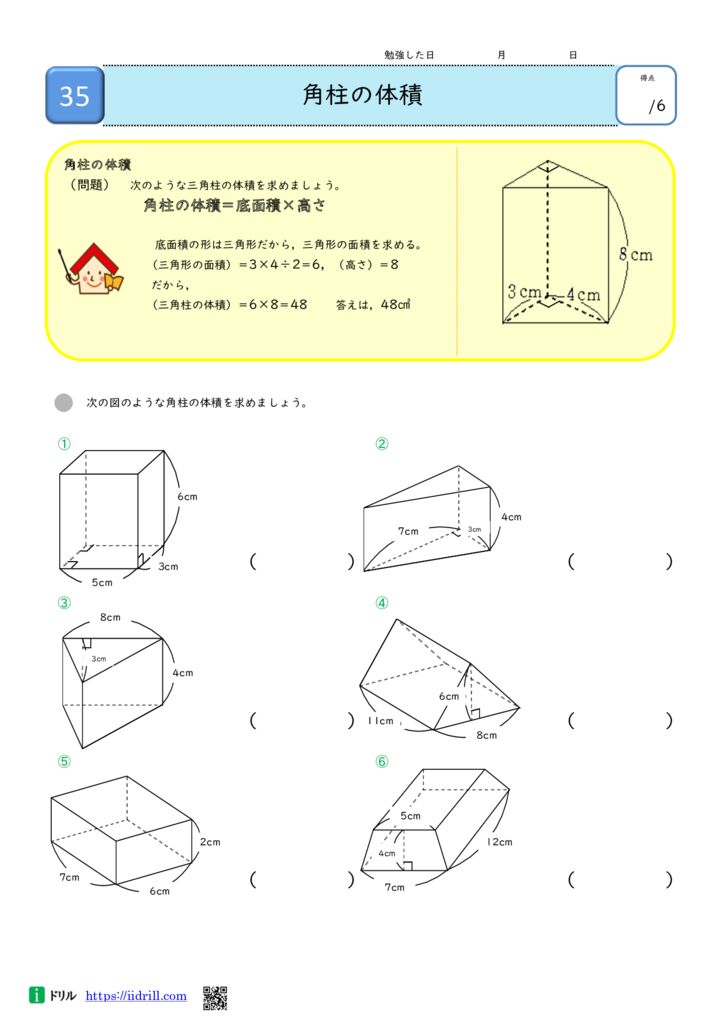
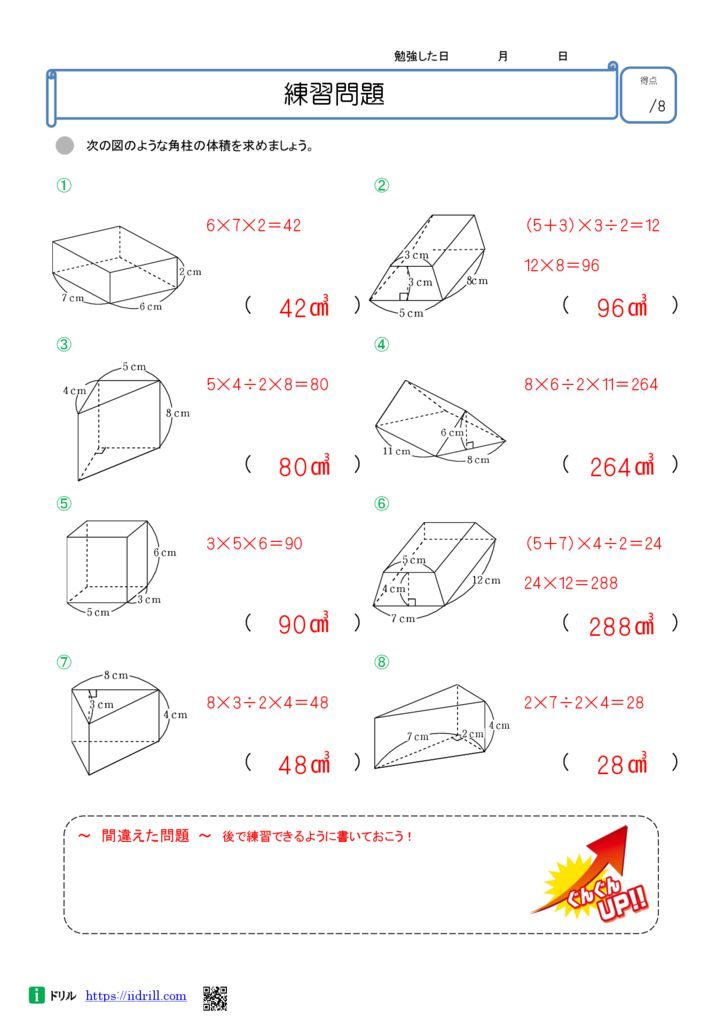
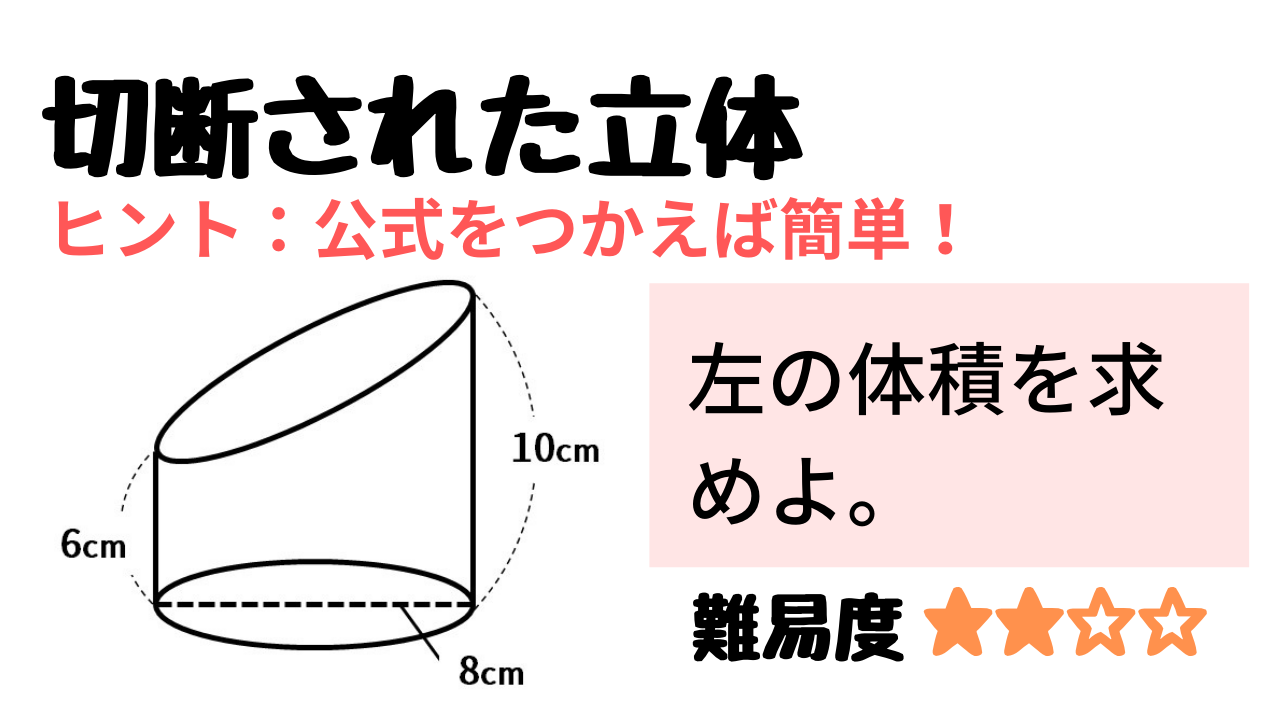
右の図は直方体を斜めに切断したものです。 この立体の体積を求めてください。 入試では非常に有名な問題で、これは次のように解くというのが「常識」のようです。 36 × 11 6 4 9 4 = 270 つまり、「高さの平均」のようなものを考えて、それを底面積とかけあわせて体積を求めるというわけです。 こうした解法を知っていると、確かに簡単に計算してHOME > 体積・弧長・媒介変数 > 体積積分(交差立体) 疑問点のお問い合わせやご注文などは、admin@KKyogokucomへお願いします。 ただし、恐れ入りますが、 御注文・お問い合わせの手順にしたがってお願い致しします。 見たことのない問題を限りなく減らすために: 立方体の体積を求める問題は、 底面積 × 高さ で求めます 底面積(9×4÷2)×高さ(6)で求めます 円柱・角柱の体積問題① 円柱・角柱の体積問題② 円柱・角柱の体積問題③ 体積問題のTOPページはここをクリック→ https//wpme/PadsCs1hR



中学数学 空間図形 体積の問題のコツ
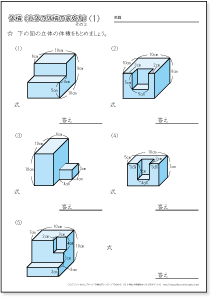



小学生の算数 図形 面積 体積 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 小学生
図形の練習問題 / 算数の成績アップ勉強法 | 年06月06日18時00分 「第499回 合否を分ける問題の解き方 立体図形の切断」 作図力が重要となる問題を、近年の中学入試の中から見てきています。 前回は「立体図形の影」をテーマにした問題について考え立体の表面積と体積の問題を見る> すべての授業の「要点まとめノート」「問題・解答」をPDF無料ダウンロードできる 学校で使っている教科書にあわせて勉強できる わからないところを質問できる 会員登録をクリックまたはタップすると、 利用規約立体の左側の高さは4cmで,右側の高さは8cmです。 底面は半径5cmの円ですから,この立体の体積は, 3)になります。 基本1 (2) ワンポイント 「平均」の高さを考えます。 立体のアの方の高さは7cmで,イの方の高さは0cm です。 そこで,この立体の高さを,7と0



すきるまドリル 小学6年生 算数 角柱と円柱の体積 無料学習プリント すきるまドリル 無料学習プリント




複雑な体積 表面積の問題 家庭教師としの勉強部屋
立方体の切断問題 できる図形 三角形,二等辺三角形,正三角形,台形,平行四辺形, ひし形,長方形,正方形,五角形,六角形,正六角形 できない図形直角三角形,直角二等辺三角形,(ただの)四角形,正五角形,七角形以上 解答1 単元名「立体の体積」 2 指導観 本学級の児童(男子19 名、女子9名)は、不えられた計算問題などの課題には一生懸命に取り組むことがで きる。全体的に見ると、習熟度に大きく差が付いており、個別に支援が必要な児童が数名いるため、年度当初よHello School 算数 体積・表面積 練習問題 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。 ※特に指定がない場合、円周率は314とします。



立体の体積を求める 苦手な数学を簡単に



無料 中1数学 標準問題 解答プリント 143 空間図形6 立体の体積



6年生算数ドリル 立体




立体の表面積と体積 の問題のわからないを5分で解決 映像授業のtry It トライイット




立体の表面積と体積 の問題のわからないを5分で解決 映像授業のtry It トライイット



6年算数立体の体積その2 教え方
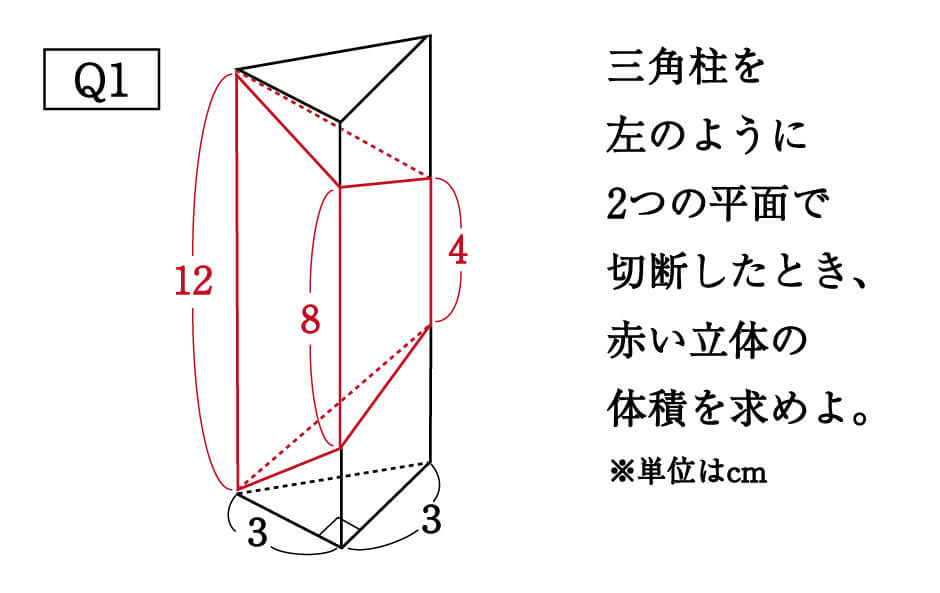



数学 斜めに切断された三角柱の体積は こう解くべし 受験の秒殺テク 7 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




すきるまドリル 小学5年生 算数 体積 無料学習プリント すきるまドリル 無料学習プリント




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



数学 斜めに切断された三角柱の体積は こう解くべし 受験の秒殺テク 7 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
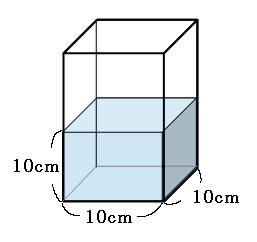



水の中に立体を入れる問題の解き方 お風呂に入るとお湯があふれるあの現象



1




6年生算数ドリル 立体




立体の体積 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生



直方体 立方体の体積 小5 きちんと式を書けば簡単 算数の教え方教えますmother S Math Happy Study Support
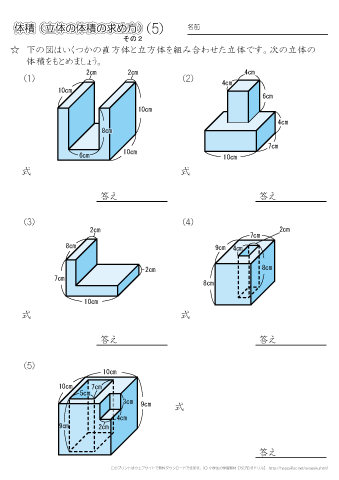



小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生



立体の体積を求める問題 回転させてできる立体 苦手な数学を簡単に



切断した立体の体積を求める総合力問題 力試し 中学数学 理科 寺子屋塾の復習サイト




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




中学1年の数学 動画 立体の体積の問題 19ch



6年生算数ドリル 立体



2




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun
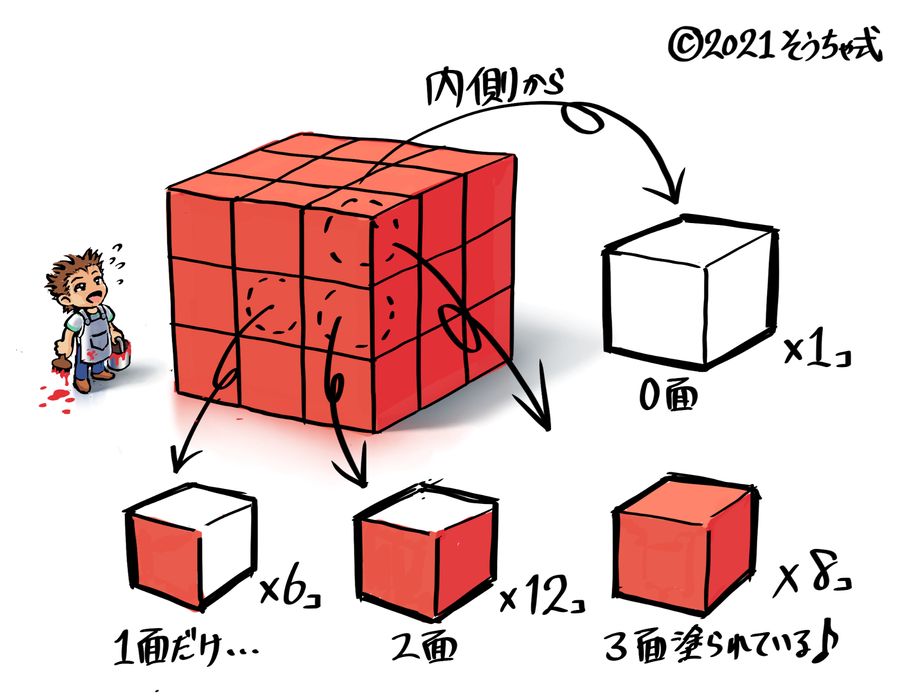



中学受験 直方体 立方体のまとめ 立体図形 そうちゃ式 受験算数 2号館 図形 速さ
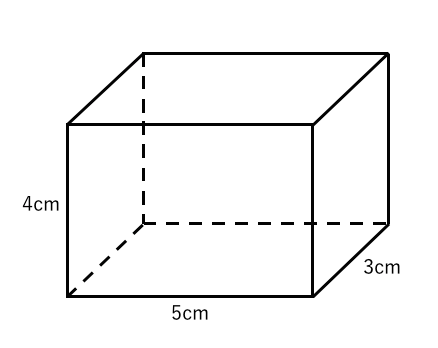



立体の表面積を求める 基本問題 苦手な数学を簡単に
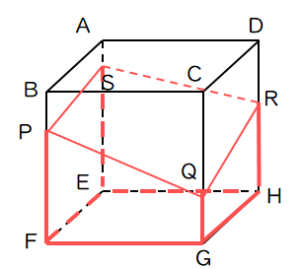



高校入試対策数学 切断した立体の体積を求める練習問題 Pikuu




中1数学 立体の体積 練習編 映像授業のtry It トライイット




立体の体積問題 12年 麻布中学校 恋する中高一貫校 適性検査 徹底攻略




立体の表面積と体積を求める問題です 分からないので教えてください Clear
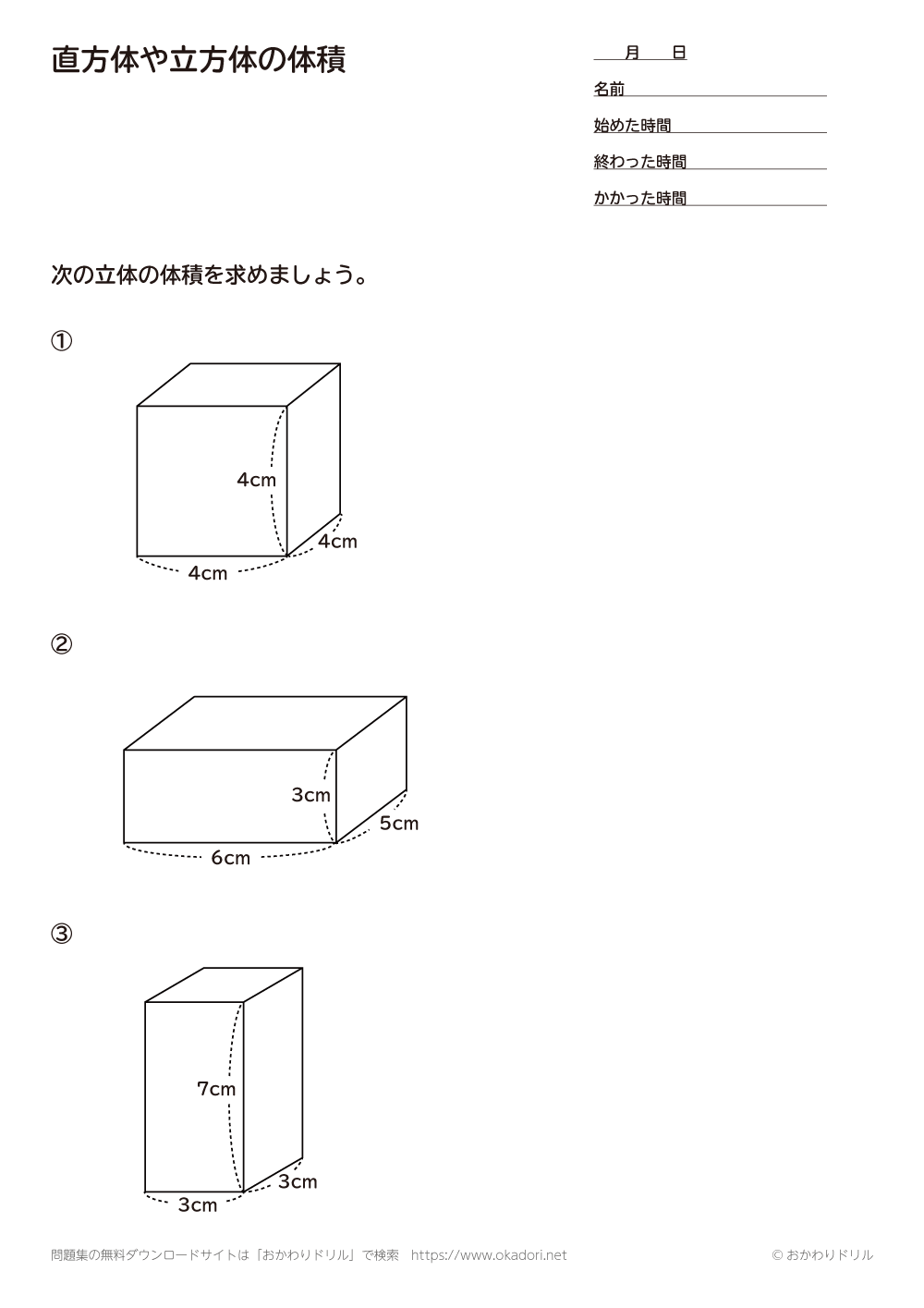



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル
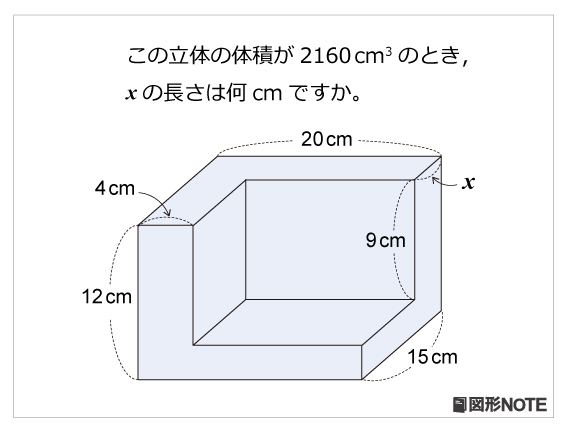



図形noteプレ レベル4 直方体の体積 算数星人のweb問題集 中学受験算数の問題に挑戦



空間図形 練習問題 4 ネット塾
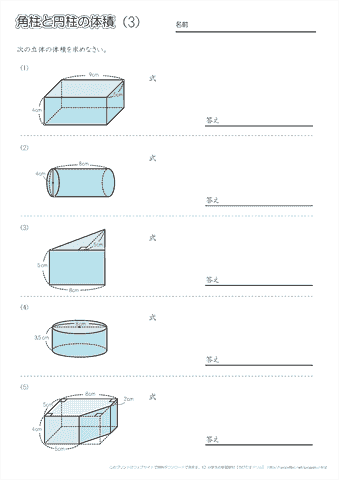



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生




直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 北辰塾 情報局
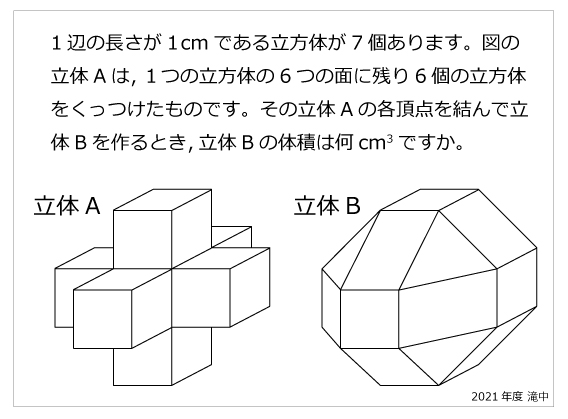



今年の1問 21年滝中 立体の体積 算数星人のweb問題集 中学受験算数の問題に挑戦
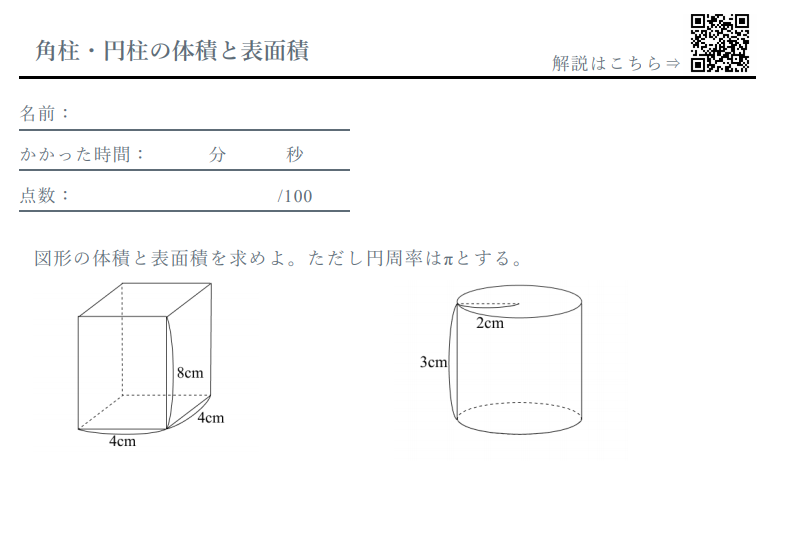



角柱 円柱の体積と表面積 計算ドリル 問題集 数学fun



6年算数立体の体積1 教え方



中学受験算数 切断された円柱 角柱の体積の問題 Stupedia




やや難しい立体の体積 Youtube




立体の体積 無料で使える中学学習プリント



立体の体積



三角柱の表面積 底面積も と体積を求める公式と計算問題 単位との関係 ウルトラフリーダム



中学1年数学練習問題 立体 円柱 三角錘 四角錘等 の体積の問題



1




立体の体積 無料で使える中学学習プリント



6年算数立体の体積1 教え方



Studydoctor立体の体積の求め方と公式 柱体 中学1年数学 Studydoctor




複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座




至急 この問題を教えてください Clear
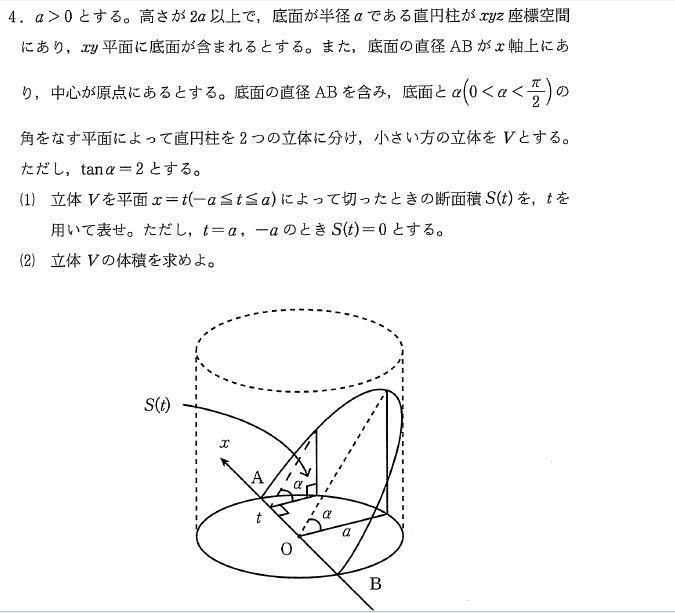



立体の断面積から切断した立体の体積を求める問題です 大学入試数学問題の解説 解答




世界一分かりやすい算数 小6 立体の体積




この問題が良くわかりません Clear




複雑な体積 表面積の問題 家庭教師としの勉強部屋



Mathematics 立体の切断 高校入試に出る難しい問題 働きアリ
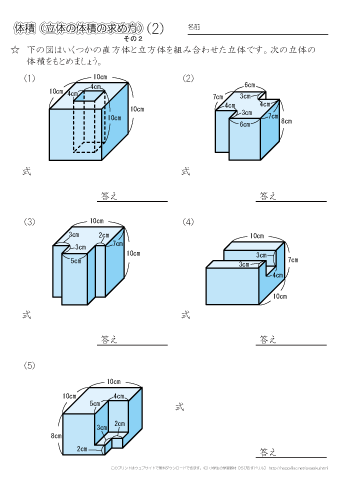



小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生
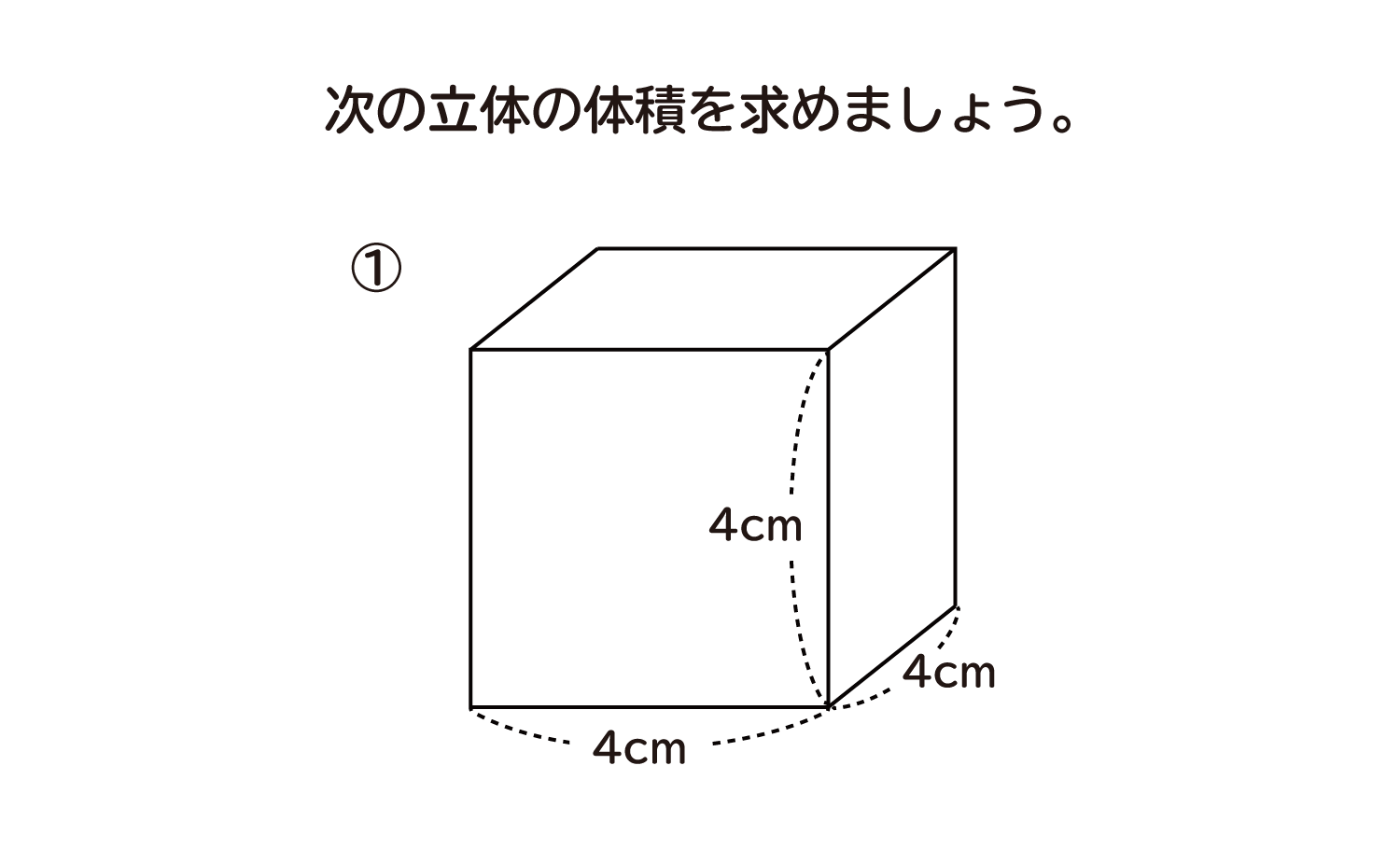



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル



Q Tbn And9gcrcfjh5dnkywzu1xman7gtxgd Ehtkomy4k80pco4m0l1tcpvuv Usqp Cau




中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生



数学の問題教えてください 立方体から切り取った三角錐の体積はどうやって Yahoo 知恵袋




立体の体積 無料で使える中学学習プリント
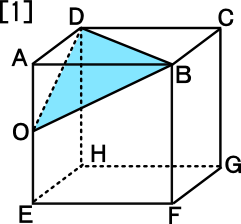



中学1年数学練習問題 切り取った立体の体積の求め方と解答



モノマナビ研究所



算数の問題です 1 図の立体は 円柱を半分に切った形です この立体の体積は何 Yahoo 知恵袋
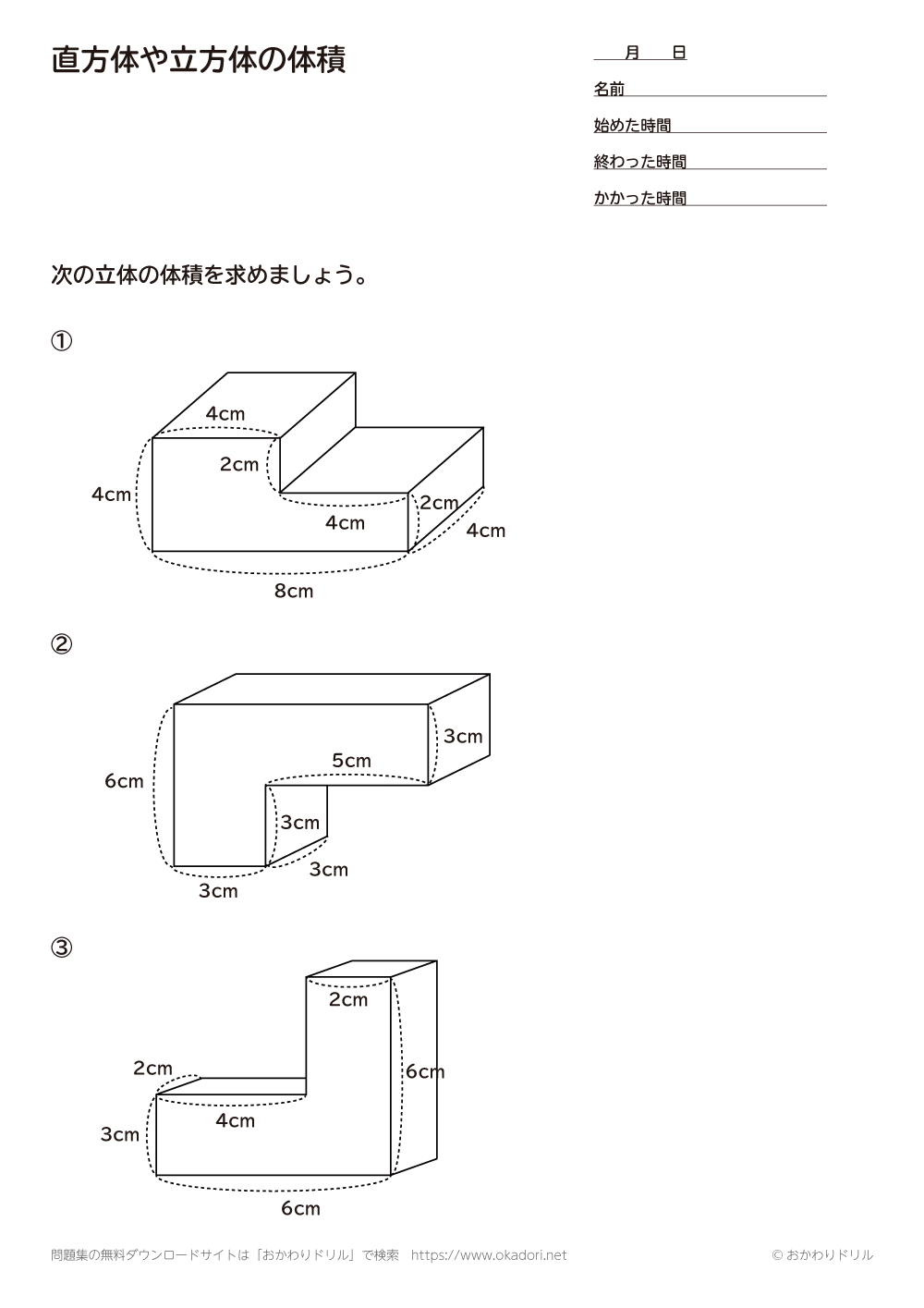



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル



点dを含む立体の体積は 今年 2018年 芝中学 どう解く 中学受験算数



無料 中1数学 発展問題 解答プリント 空間図形6 立体の体積




表面積と体積の比の問題 立体の相似比を出すのが一番最初だ 中学や高校の数学の計算問題




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム



無料 中1数学 基本問題 解答プリント 空間図形6 立体の体積 143




中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
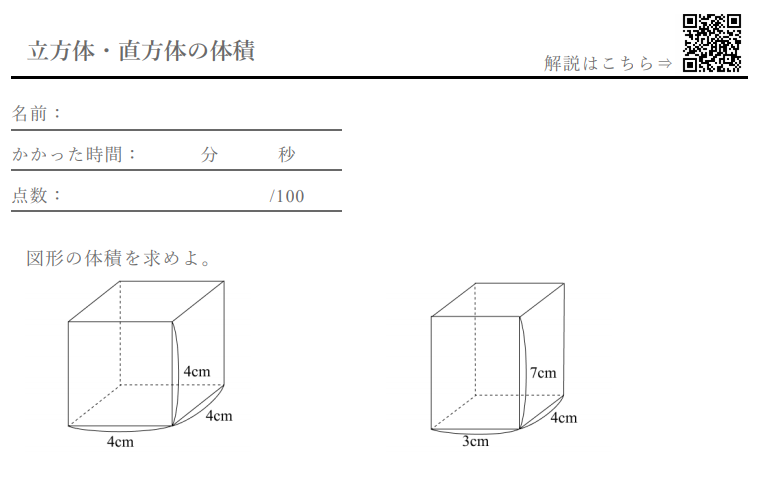



立方体 直方体 の体積 計算ドリル 問題集 数学fun




直方体の体積に関する問題 11年 桜蔭中学校 恋する中学受験 大学受験を見据えた中学受験




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun
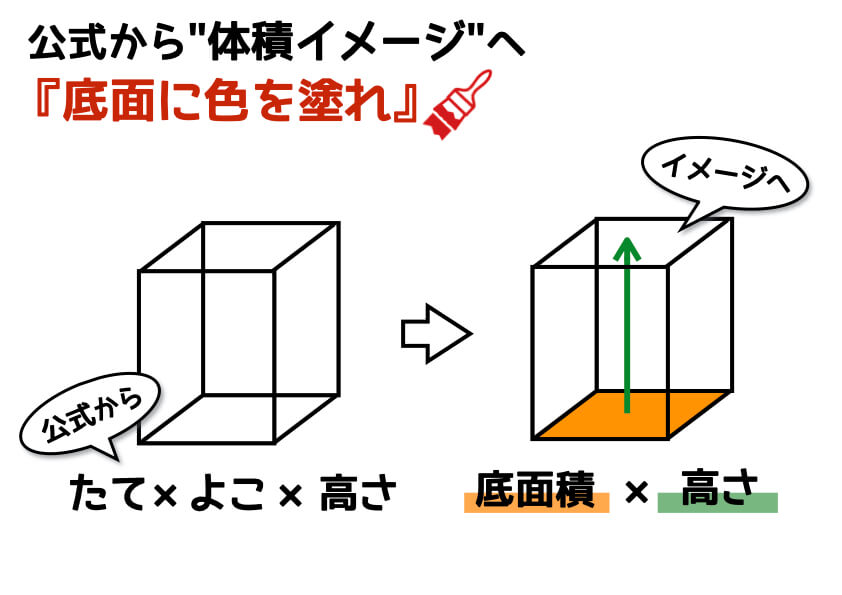



小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ
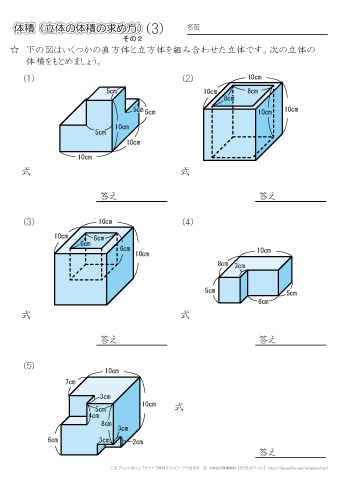



小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生



算数の問題です 解答を教えていただけませんか この図の立体は 直方体 Yahoo 知恵袋



立体図形の体積 第19問 女子学院中学 09年 平成21年度 受験問題 算数 まいにち一題 中学受験過去問題研究
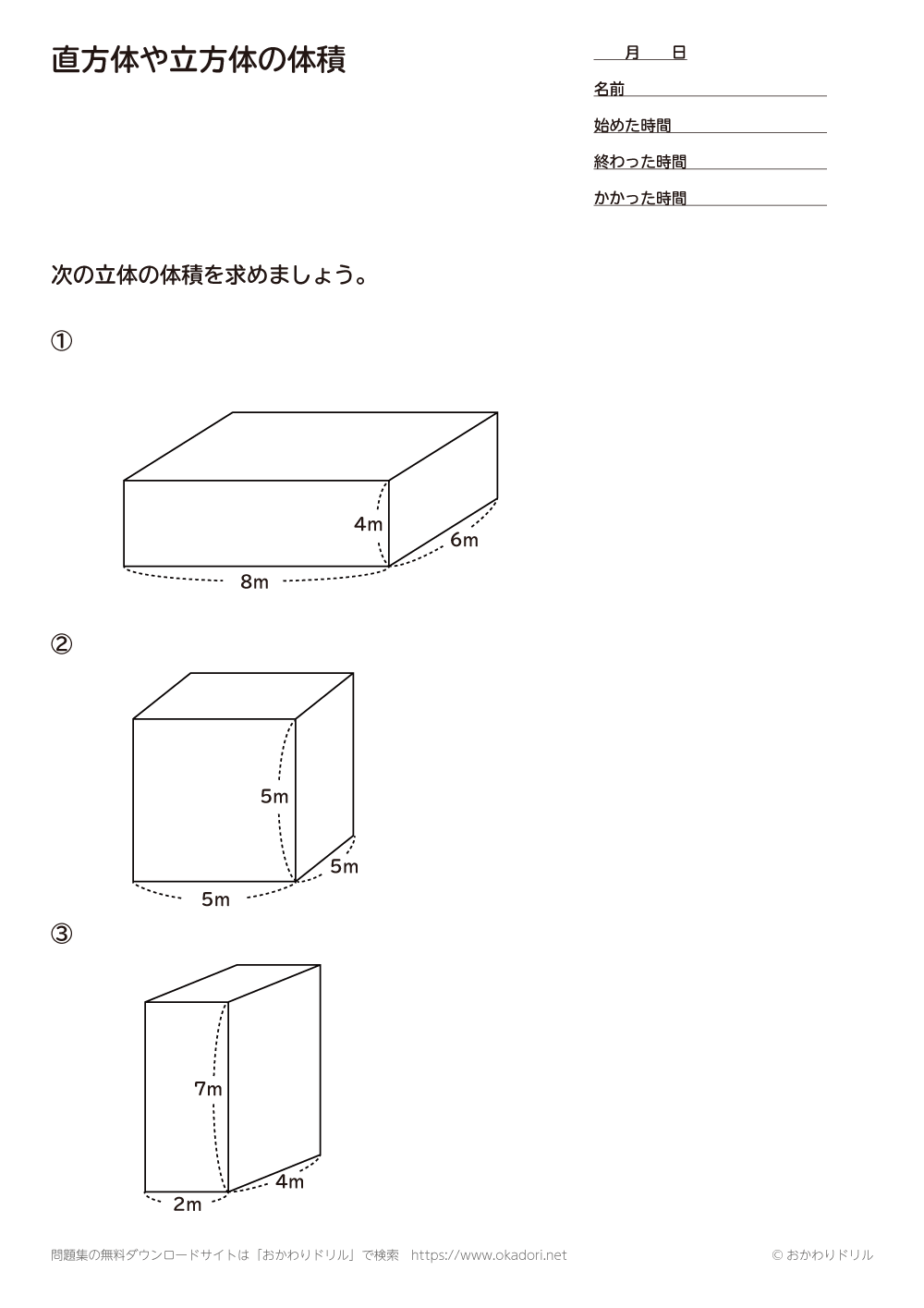



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル




角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun



三角柱とは 体積 表面積の公式や求め方 計算問題 受験辞典
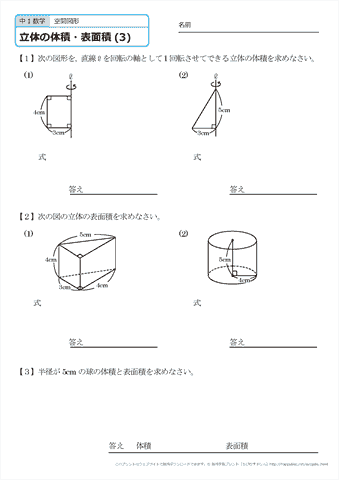



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
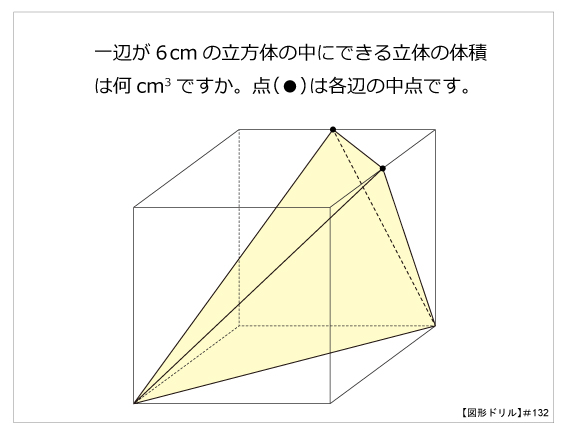



図形ドリル 第132問 立体の体積 算数星人のweb問題集 中学受験算数の問題に挑戦
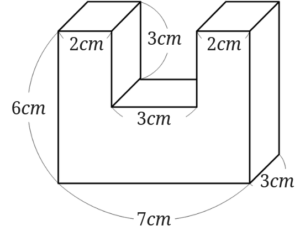



直方体や立方体の体積を求める応用問題の解き方は どうやって教えるといいの みけねこ小学校



Q Tbn And9gcrcfjh5dnkywzu1xman7gtxgd Ehtkomy4k80pco4m0l1tcpvuv Usqp Cau



無料 中1数学 基本解説 問題プリント 空間図形5 立体の体積 143
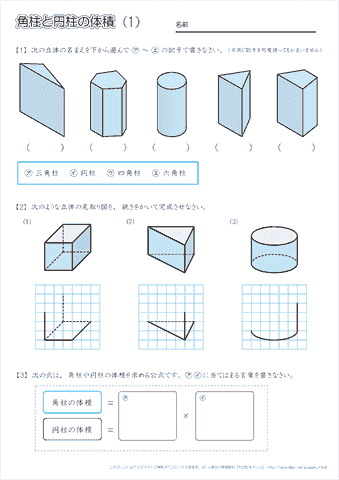



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生
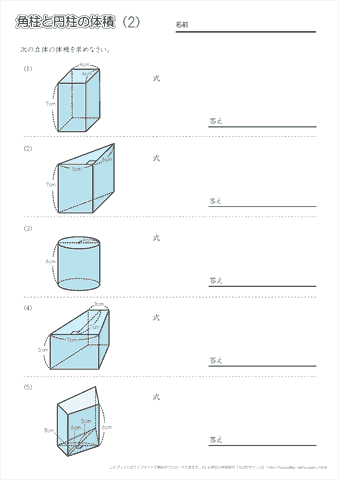



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生




世界一分かりやすい算数 小6 立体の体積



0 件のコメント:
コメントを投稿