
必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ
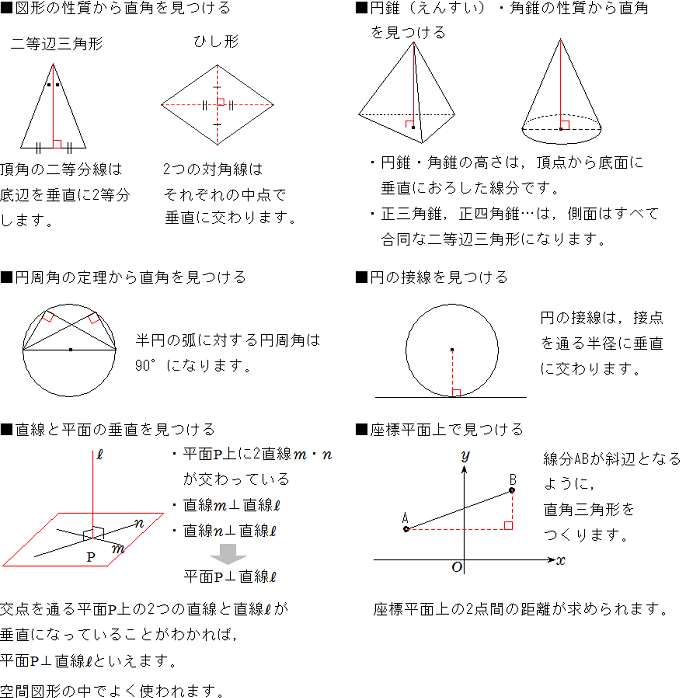
直角三角形の辺の長さを a、b、c (斜辺) とすると、a2+b2=c2 の関係になっています。この関係を三平方の定理といいます。*ピタゴラスの定理ともいいます。直角三角形において、斜辺(1番長い辺)の2乗は、残りの2辺のそれぞれの2乗の和に等しい証明のやり方三平方の定理の三平方の定理が使えるのは直角三角形である。 定理を利用する場合は図から直角三角形を探すか、補助線を書いて直角三角形を作る。 座標上での2点間の距離 いままで、座標上で斜めの長さは出せなかったが、三平方の定理を使えば出せるようになる。 a b
中学 数学 三 平方 の 定理
中学 数学 三 平方 の 定理-中学数学 中学数学三平方の定理授業編 『三』平方なので3つの2乗の数の関係式ということです。 今回は中学数学の連立方程式をやっていきます。 中学2年生がメインターゲットですが、1年生の人は予習、3年生の人は復習に役立ちますよ。数学中361 三平方の定理①(基本編) Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device

三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張
ツイート 中学3年生の数学 練習問題プリントです。 家庭学習用の練習プリントとして、またテスト前の確認などにもご利用ください。 式の展開と因数分解 平方根 2次方程式 2次関数 図形の相似 三 三平方の定理を使って面積を求める方法は? 問題を使って解説するよ! 次の三角形の面積を求めましょう。 まず、底辺を6㎝とした場合の高さとなるような線を引きます。 すると、三角形が2つの直角三角形に分けることができますね。 そこから左に 数学の知識のなかには、これさえ乗り切ればあとはいくらでも応用がきく、というものがあります。 そのひとつが 三平方の定理 です。 三平方の定理は中学校で習う内容ですが、 これをしっかり理解しておくと、高校の数学の授業が面白いように頭のなかに入ってきます。
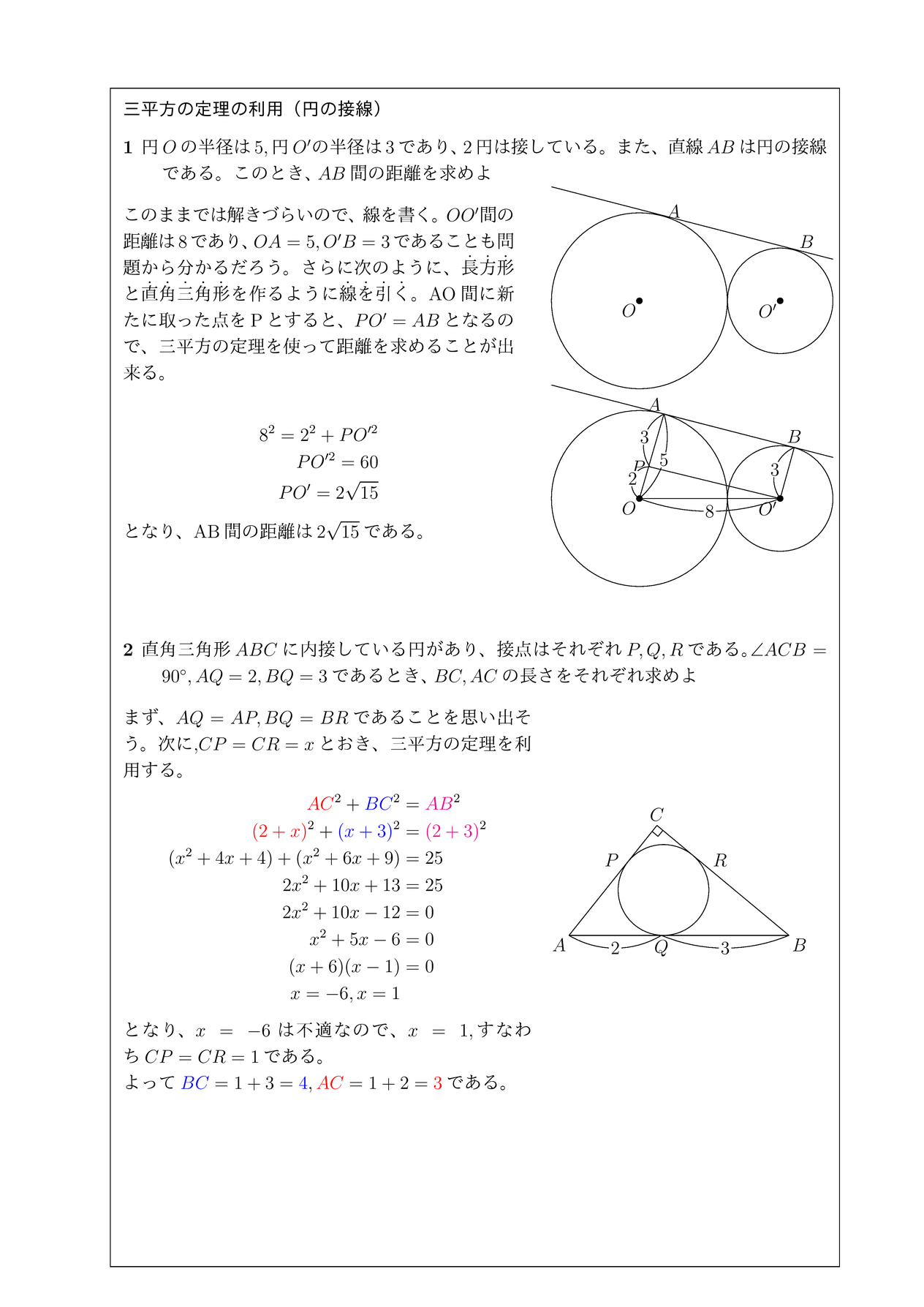
つまり、下図のようになるよ! ということは、各頂点から点Pまでの長さが 6 6 だから、三平方の定理を用いると、 x2 = 62 –22 x 2 = 6 2 – 2 2 ∴ x2 = 36− 4 = 32 x 2 = 36 − 4 = 32 ∴ x = 4√2 x = 4 2 (x>0より) これを図にするとこう! 終わり! はかせちゃん お疲れ円外の点から円に接線を引くとき、左右対称な 2 2 本の接線が引けます。 どちらで解いても関係ないですね。 求める半径の長さを x x とすると 三平方の定理より x2 122 = 162 x 2 12 2 = 16 2 x2 144 = 256 x 2 144 = 256 x2 = 112 x 2 = 112 x = ±√112 x = ± 112 = ±4√7 = ± 4 7三平方の定理中学3年生 数学基本と重要ポイント 今回は「三平方の定理」の基本から重要なポイントまでお伝えしていきます。 三平方の定理の問題が解けない! という人、しっかりと理解して、問題が解けるようにしていきましょう! このページの
中学 数学 三 平方 の 定理のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 | 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 | 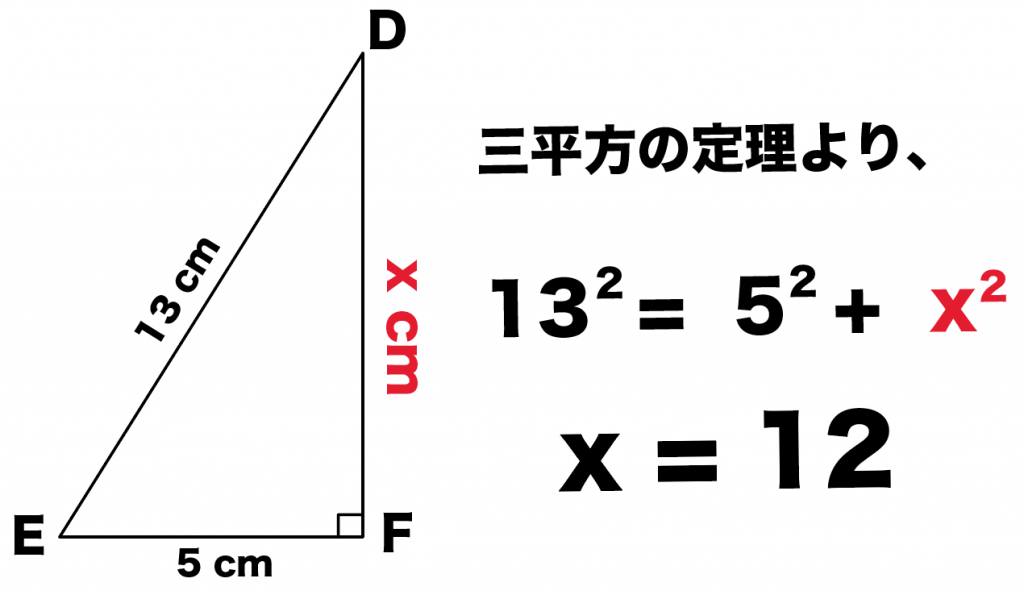 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 | 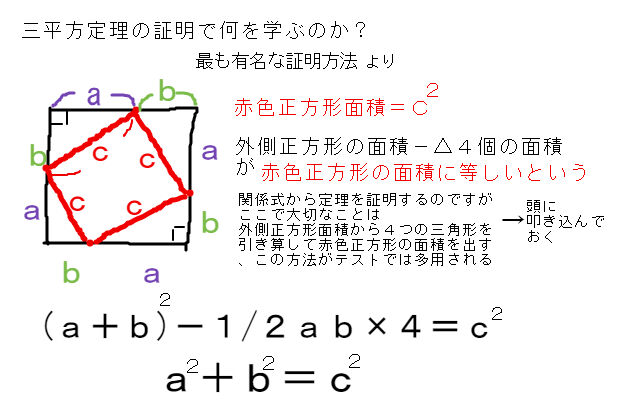 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
「中学 数学 三 平方 の 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 | 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
「中学 数学 三 平方 の 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
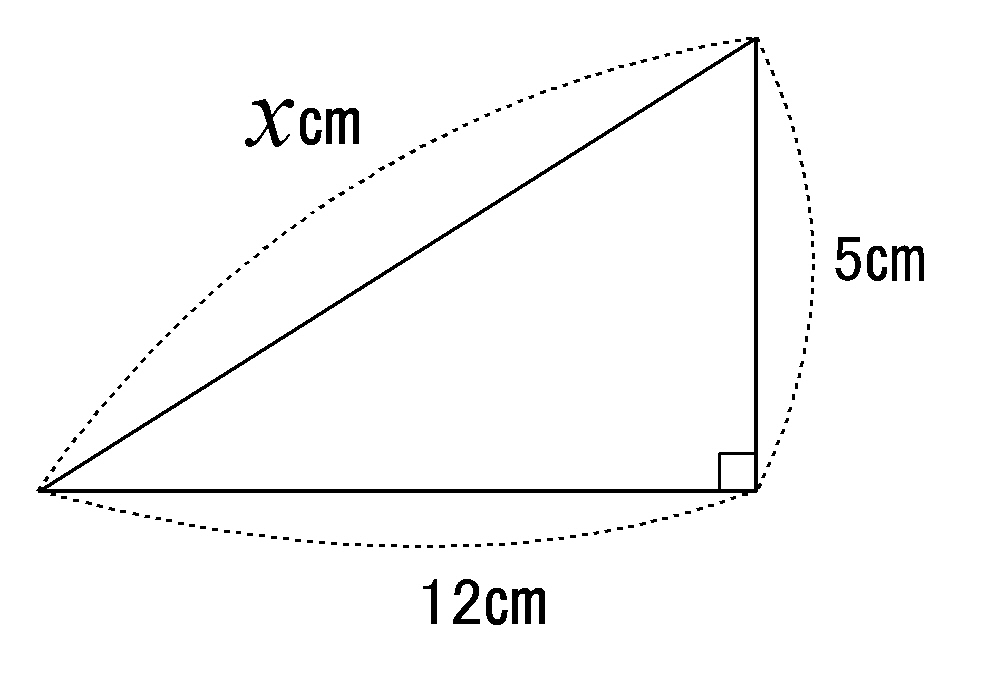 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 | 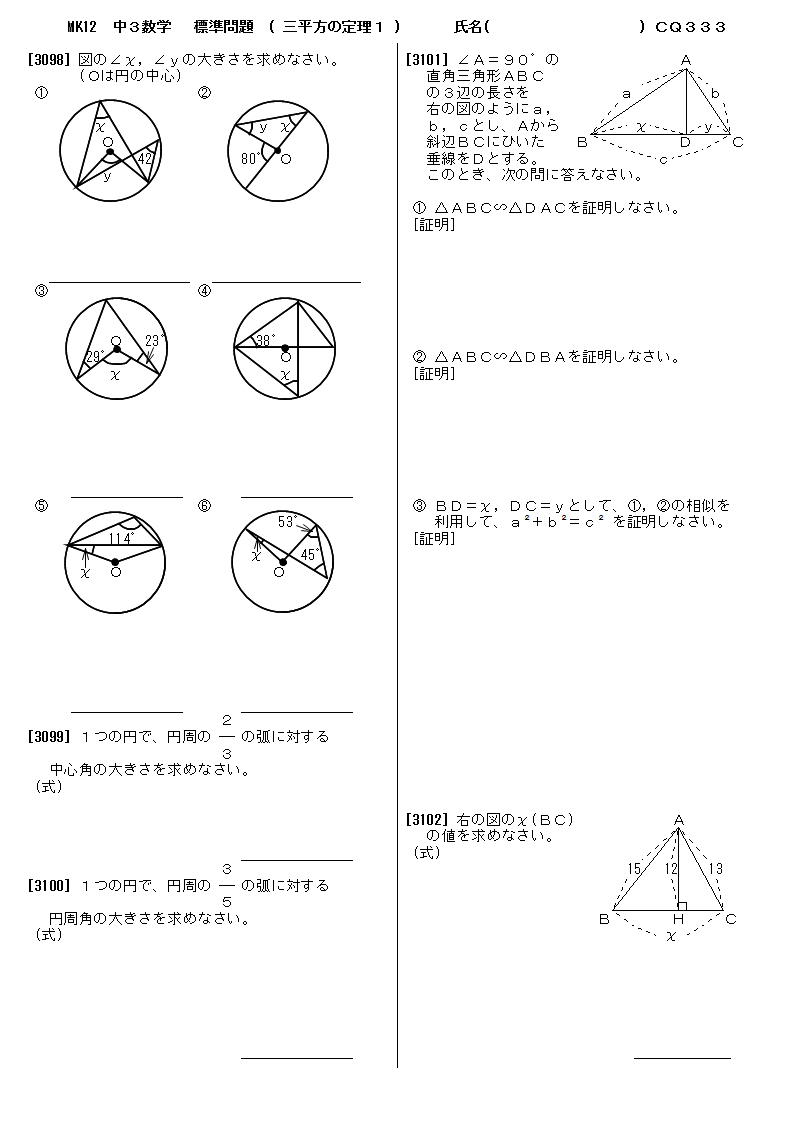 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 | 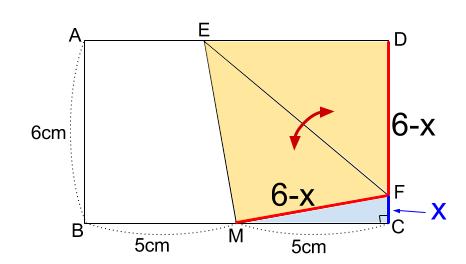 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
「中学 数学 三 平方 の 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
「中学 数学 三 平方 の 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 | 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 | 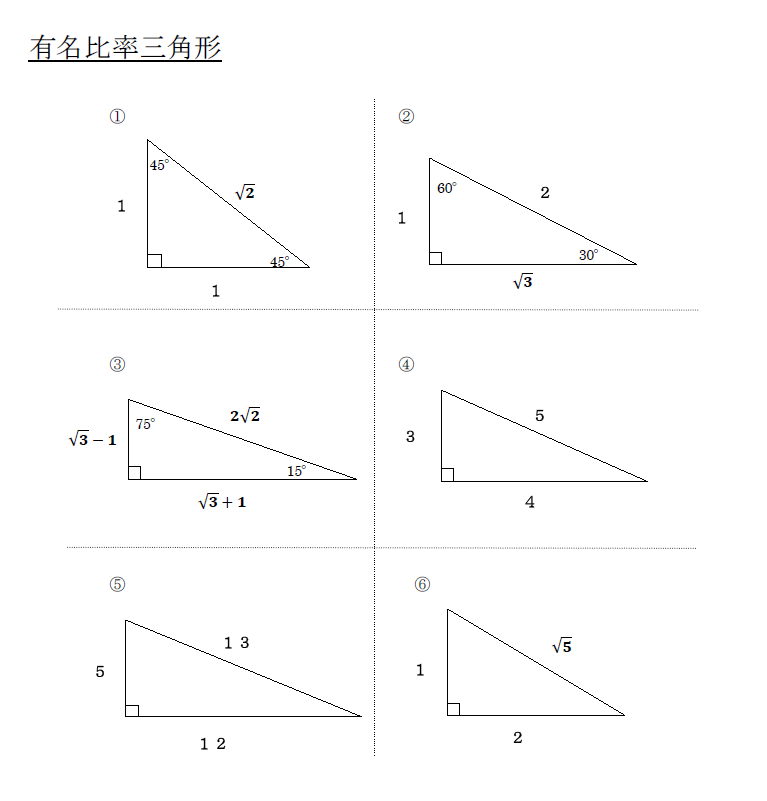 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
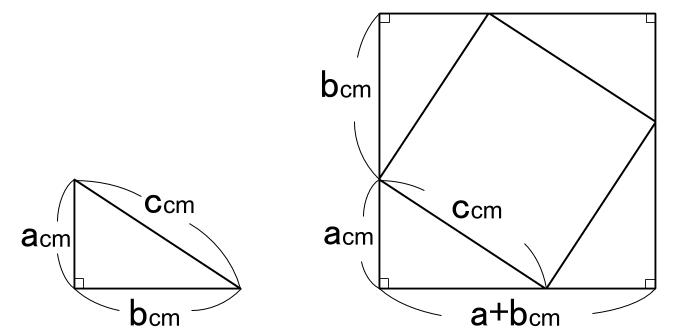
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
「中学 数学 三 平方 の 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
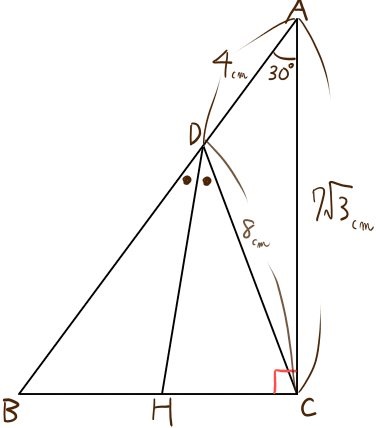 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 | 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
「中学 数学 三 平方 の 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
「中学 数学 三 平方 の 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 | 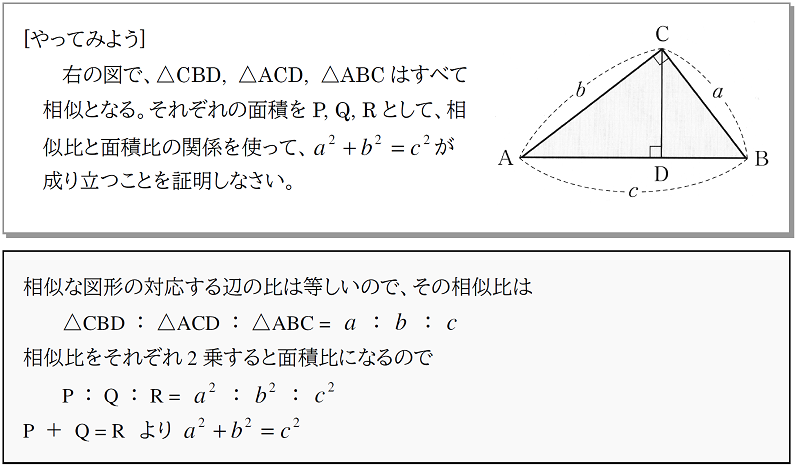 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 | 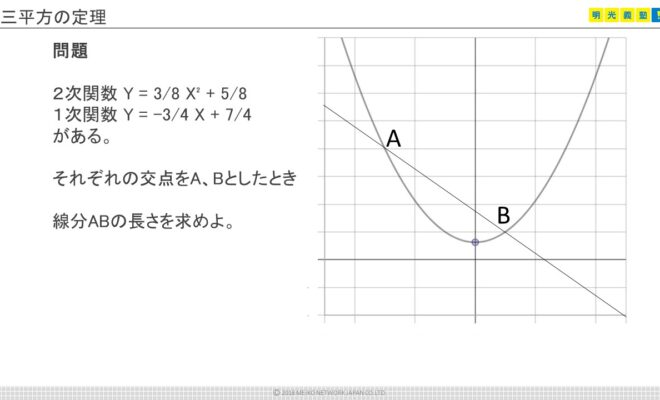 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
「中学 数学 三 平方 の 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 | 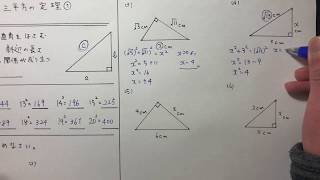 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 | 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 | 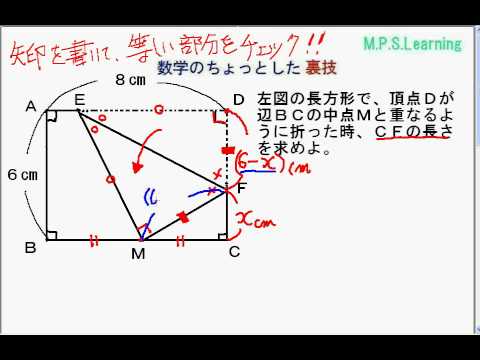 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
「中学 数学 三 平方 の 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
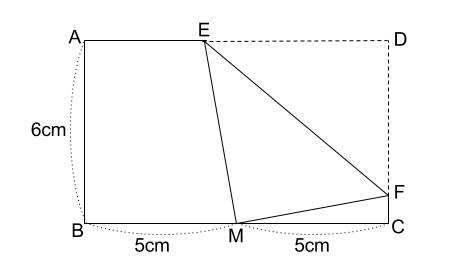 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 | 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 | 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
「中学 数学 三 平方 の 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 | 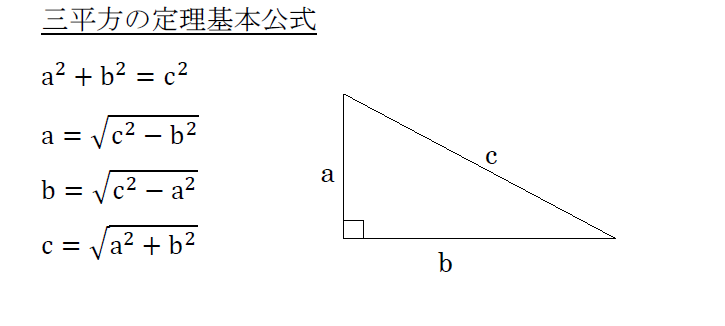 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 | 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
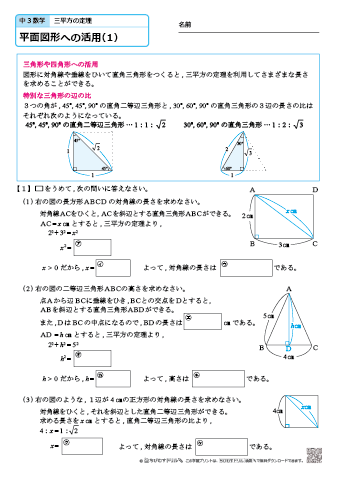 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |  三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 | 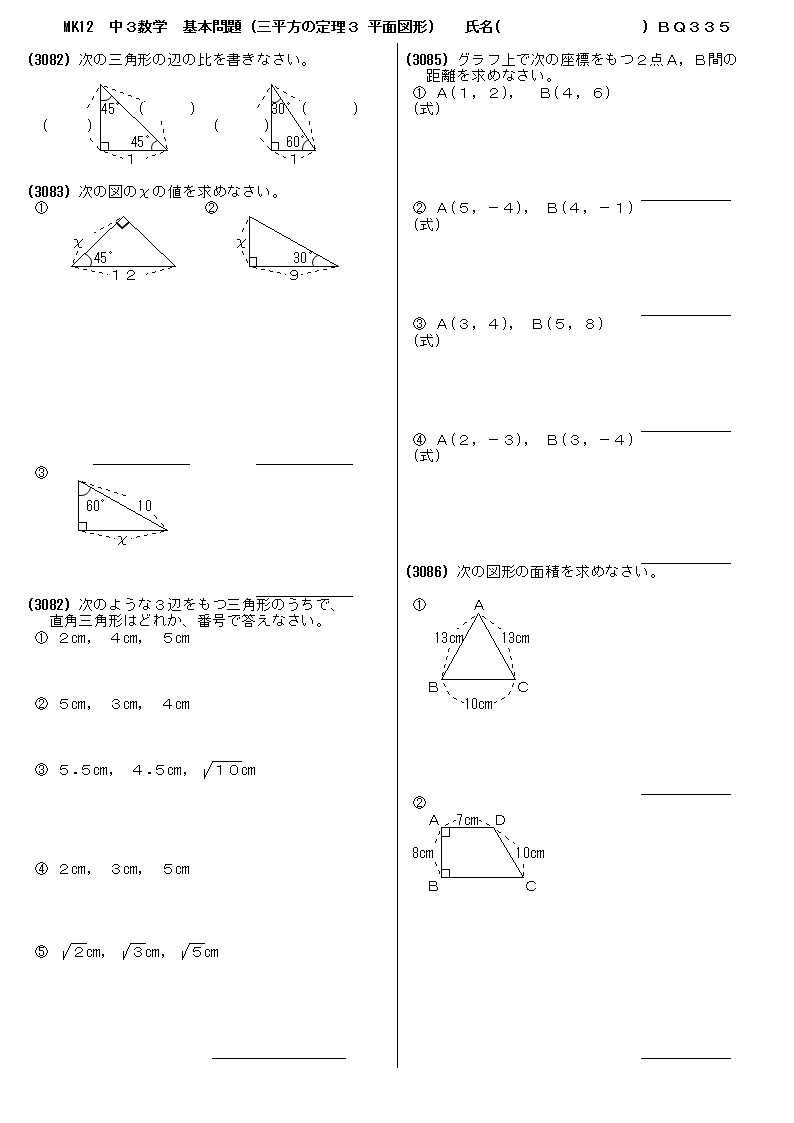 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
「中学 数学 三 平方 の 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 | 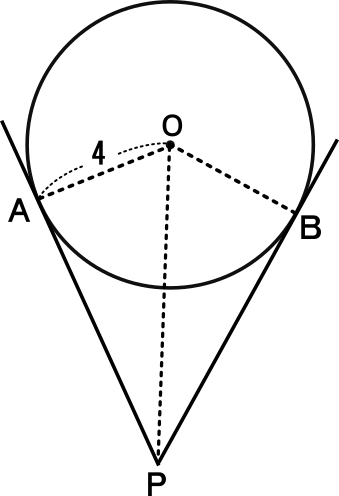 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 | 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 | 三平方と二等辺 36 平面図形 オリジナル 高校入試 数学 良問 難問 |
Pocket 中学数学で学習する重要な公式たちをまとめておきます。 入試や学力テストなど 大きなテストの前には、こちらの記事で公式をチェックしておきましょう (^^) こちらのページで紹介している 公式をまとめたプリントを無料でプレゼント! 印刷して三平方の定理とは 三平方の定理(基本問題1) 例題と練習 三平方の定理(基本問題2) 例題と練習 三平方の定理(四角形の対角線) 例題と練習 特別な三角形 例題と練習 特別な三角形2 例題と練習 二等辺三角形の面積 例題と練習 三辺から三角形の面積を求める 例題と練習 座標上の2点間の距離 例題と





0 件のコメント:
コメントを投稿